この記事は新歓ブログリレー2019 3月14日(6日目)の記事です。
受験生の皆さん、受験お疲れ様でした!東工大2015年度入学のnariです。
一段落したところかと思いますが、入学手続きや住まいの手続きなどあるかと思います。
私も東工大の大学院に進学するため、卒業と入学の手続きなどがいっぱいで大変です。
くれぐれも期限に遅れないよう、また季節の変わり目ですから体調にも気をつけて、新年度の準備を進めていただければと思います。
さて、3月14日といえばアレですね。
円周率の日ですね。
円周率といえば3.141592...で有名な無理数で、東工大内のいたるところで「円周率を何桁言えるか?」でマウントの取り合いが発生したりしてますね(してません)。
受験の際には と表記すれば良いためあまり使いませんが、これを読んでいる皆さんの中にも、ふとこの永遠に続く円周率を覚えてみようと頑張った経験のある人は多いんじゃないでしょうか。
え、3月14日といえばホワイトデー?そうですか。
ホワイトデーといえばバレンタインデーのお返しとしてプレゼントを贈る日です。そこに込められている気持ちがなんであれ、普段思っていることをプレゼントを介して伝えるということはとても大事なことだと思います。そういった習慣が永遠に続くといいですね。知らんけど
ん?
永遠に続く……?
……というわけで、今回は永続データ構造についてお話したいと思います。
はじめに: この記事について
この記事では、プログラミングにおける高度なアルゴリズムの話を行います。
新入生歓迎ブログリレーという名とは裏腹に、現役情報系学生でも理解しづらい記事になるかと予想されます。
そこで、予めこの記事のあらすじをざっくり紹介し、想定される対象読者を示します。
この記事のあらすじは以下の通りです。
- はじめに(イマココ)
- データ構造の説明
- 永続データ構造の説明
- 永続データ構造のうちの永続配列の実装方法
- 競技プログラミングのちょっとした紹介
- おわりに
この記事の想定読者は以下の通りです。
- AtCoderとかに登録してバリバリ競プロやってるぜー!な人
- アルゴリズムの勉強にお役立てください
- アルゴリズム詳しくないけどちょっと勉強してみたいな……な人
- 比較的平易な言葉でご紹介するので興味があれば是非
- 関数型プログラミング/永続 というキーワードに興味がある人
- 関数型言語はその性質のため永続データ構造が基本となります
- サークルtraPの雰囲気が知りたい人
- こういう人もいるんだよ~という参考になれば幸いです
- 今後のブログリレーでも癖の強い人が大勢出てくると思いますがゆっくりしていってね
逆に想定していない読者は以下の通りです。
- プログラミングを初めよう!と思っている人
- この記事はあまりにも早すぎます。この記事の摂取によって発生する困惑・知恵熱その他症状について当方は責任を負いかねます。ご了承ください。
- 永続データ構造でも永続配列以外に興味があった人
- 永続配列は永続配列でも より速い永続配列をお求めの方
- 本記事では完全二分木を利用した永続配列のみを扱います。
- 永続データ構造マスター・誤字脱字発見プロフェッショナル
- 間違いや誤字脱字がありましたら記事下部のコメント欄、もしくは Twitter:@_n_ari までご連絡ください><
データ構造について
まず、永続データ構造の前にデータ構造についての話を少しだけしましょう。
パソコン、ひいてはCPUとメモリの仕組みについてご存知でしょうか?0と1だけで処理が行われるという世界のことです。
パソコンの中では、CPUという脳が計算処理を行います。そしてメモリという場所にデータを保存します。
メモリは一次元上に並んだ箱の列のような状態になっていて、それぞれの箱に番地(住所のようなもの)が連番で振られています。
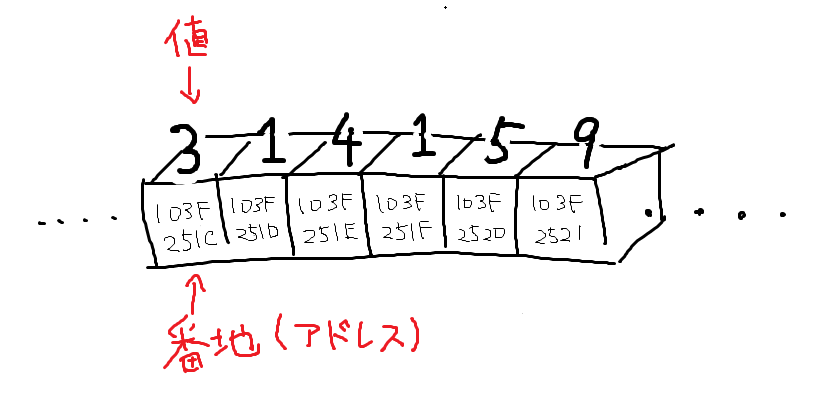
パソコンでは基本的にこのメモリ上にデータを保存し、このデータをCPUが読んだり書いたりして処理を行います。
ただし、メモリの箱1つには基本的に小さい数字(0から40億ぐらいまで)しか入りません。
知ってる人向け: 32bitの世界ということにしといてください
ここで、プログラムの使われ方を考えてみましょう。
例えばいまこの記事に連なっている文字の列。文字自体はASCIIコードやUTF-8エンコードなどで数字と対応できるので、1文字ならメモリの箱1つに収まります。が、10文字、100文字となると1つの箱では足りません。どうやってパソコンで処理しているのでしょうか?

例えば「ニューラルネットワーク」と呼ばれるものではネットワーク構造を考えて処理を行います。が、メモリは先程言ったとおり一次元に並んだ箱の列でしかありません。こんなに複雑なネットワーク構造をメモリ上で表現するにはどうすればいいのでしょうか?
……などなど、メモリの箱1つ、数字1個で表現できない構造を持ったデータを扱う必要が、プログラムを書いて問題を解決するにあたってたくさん出てきます。
このような場合にプログラマが使う・作る必要があるのが、データ構造と呼ばれるものです。
代表的なデータ構造
では、データ構造の内、よく使われる・知られるデータ構造として、配列とリストを紹介します。
配列
配列とは、データを1列にまとめたものです。例えば数字の配列なら次のような感じでメモリ上に存在します。
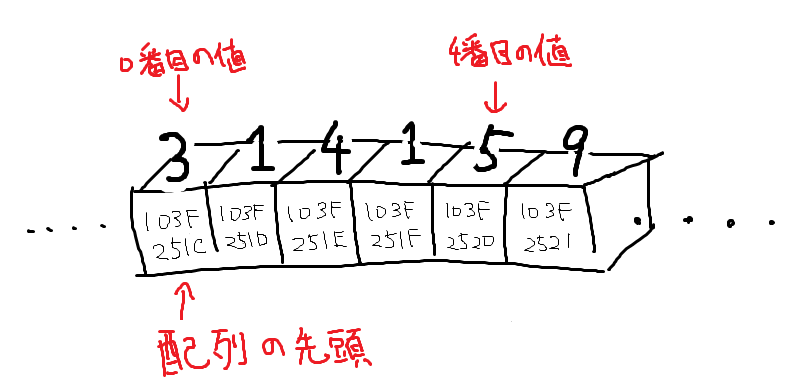
……そう、数字の配列とはまさにメモリそのものです。メモリの連続した一部分を取ってくることで配列を作ることができます!
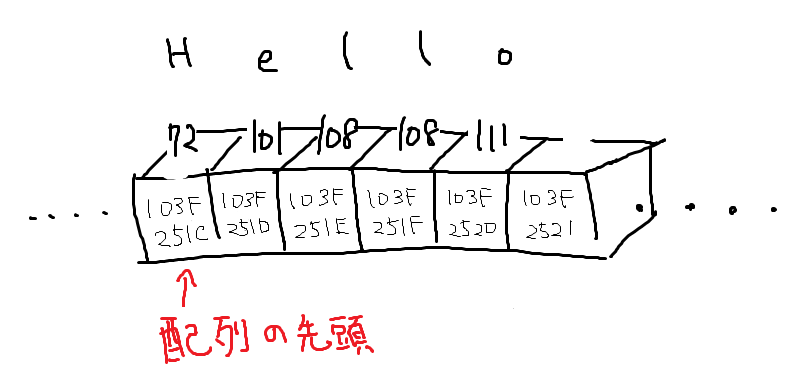
また、文字を羅列したもの(文字列)は文字の配列と見ることができます。
配列の1つのアイテムは1つの箱である必要はありません。例えば「年齢」「身長」「体重」をひとまとめにしたアイテムを考えて、その配列を作ることもできます。
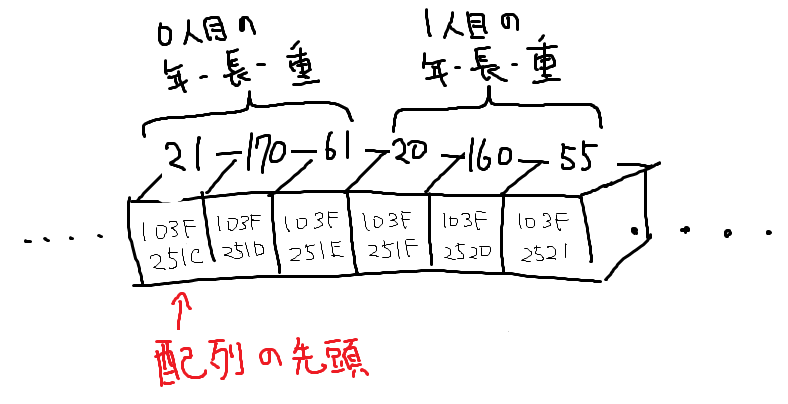
さらに特殊ですが、「配列の配列」ということもできます。メモリには番地というものが振られていたので、この数字を使って作ることができます。
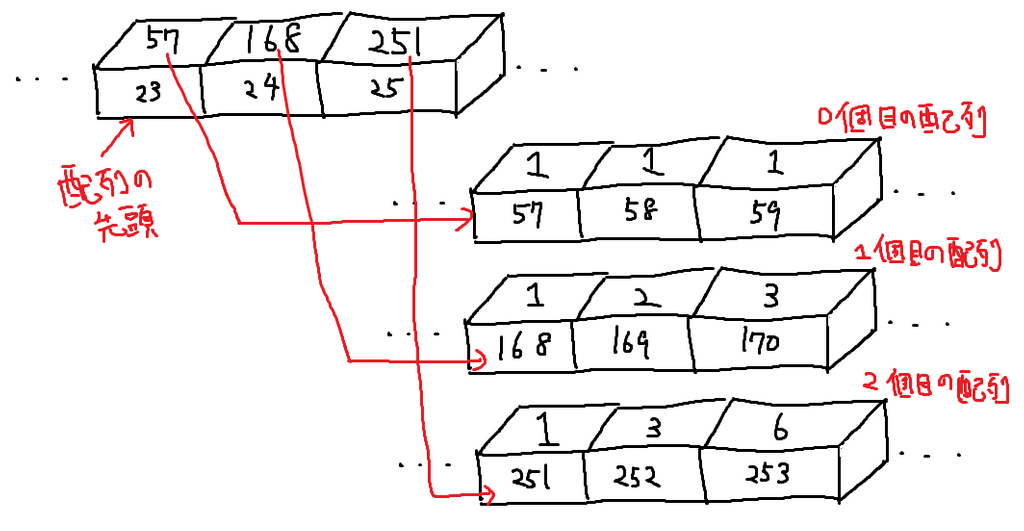
例えば(0から数えて)1番目の配列の(0から数えて)2番目の値が欲しい場合、「配列の配列」を見て1番目の配列の番地を見て、その番地にある配列を見て2番目の値を取り出す、ということで達成できます。
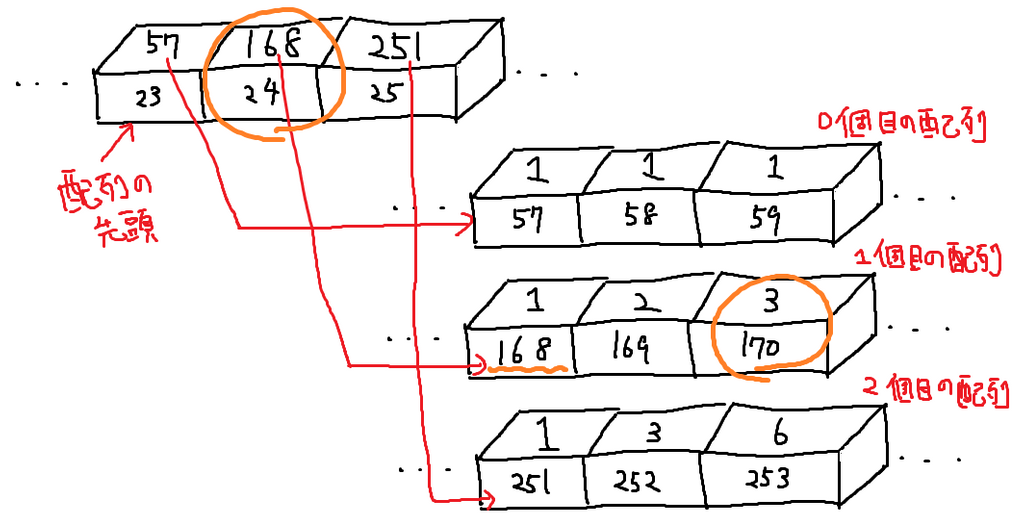
蛇足: これはまさにポインタと呼ばれ多くの初心者に恐れられているものです。仕組み自体はとってもシンプル。
メモリの連続した領域に確保された配列というデータ構造は、任意の位置の値をたかだか定数回のCPU処理で取り出すことができます。
これはそもそもメモリの番地を指定してアクセスする、という命令をCPUが持っているからです。配列の先頭の番地をしっていれば、そこに位置の分だけ足し算すれば、欲しいメモリの番地がわかりますね。
蛇足: これもまさに配列が実質ポインタと呼ばれる理由です。
たかだか定数回の処理時間のことを の処理時間、と表記します。これはランダウの記号で、 と表記したら の定数倍で抑えられる、ということを表します(厳密な定義はWikipediaや教科書等を参照)。 は の定数倍なので、別の要因によらず定数回の処理で行える、という表現になります。
ただし、配列の長さを変えたり、配列の途中に値を入れる、ということは効率よくできません。配列を1から作り直さないと実現できないことが多いです。
なんで?かというと、パソコン1つに対してメモリは1つしか無いので、プログラムはメモリを自由に読み書きはできなくて、予め宣言した分の領域しか使えないようになっているからです(配列の前後に他のプログラムのデータが入っているかもしれないので)。
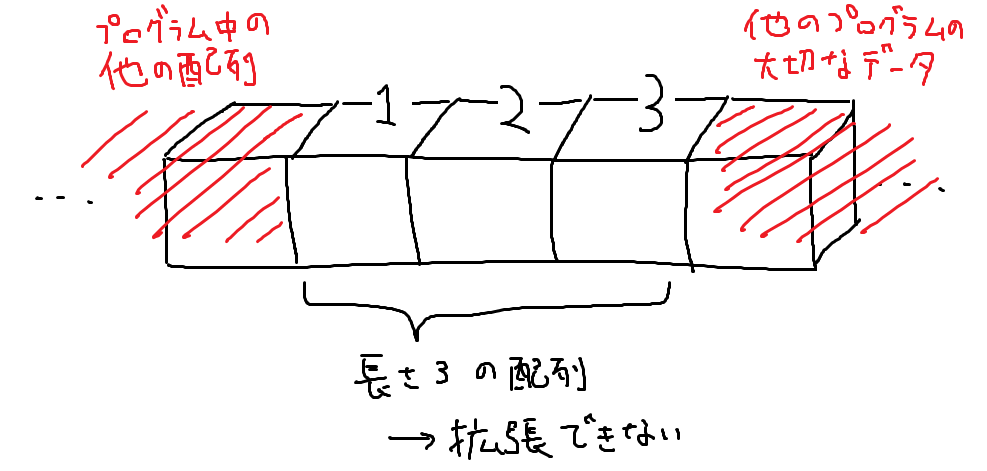
なので領域を拡大するというのも難しくて、大きい領域をもう一回確保し直してそこにコピー、みたいなことをしないといけなかったりします。
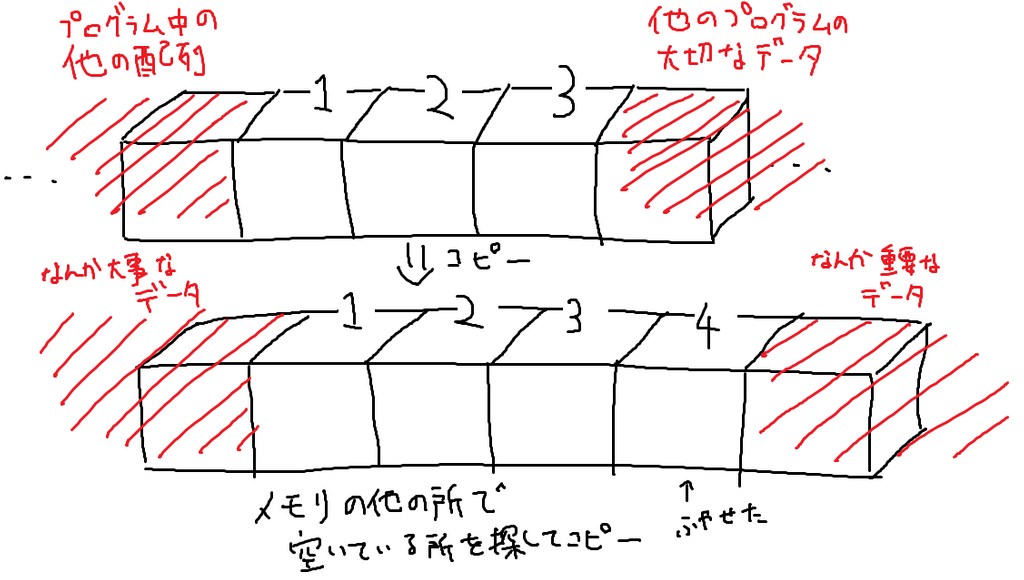
この時の計算時間は、ランダウの記号を使えば、長さ の配列に対して の計算時間がかかる、ということになります。
知ってる人向け: 配列の先頭や末尾に値を amortized で付け加える事のできる配列も存在します(可変長配列、可変長配列によって実装されたdeque)。この記事では扱いません。
リスト
リストは、配列とは別の方法でデータを1列にまとめるデータ構造です。
「配列の配列」で表したように、メモリの値としてメモリ番地を入れておくことで、あたかも矢印が張ってあるかのような表現が出来るのでした(ポインタ)。
これを利用し、1つのアイテムを次の情報で表現するものがリストです。
- アイテム自体の情報(数字、文字、データ etc.)
- 次のデータが入っているメモリ番地
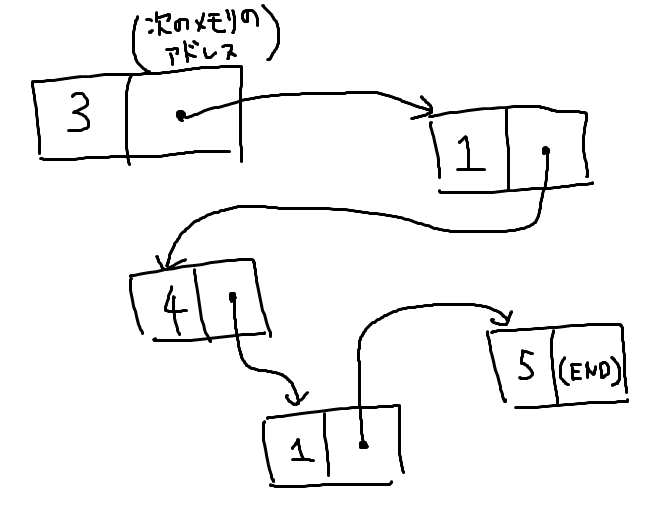
これをリストと呼びます。
リストには、配列にはあった「メモリ上に連続して存在しなければならない」という制約がありません。なので、先頭や末尾や、途中に新しいアイテムを追加することも簡単にできます。
たとえば 3 1 4 1 5 というリストを、3 . 1 4 1 5 9 と変更すると次の図のようになります。変更点がほとんど無いことがわかると思います。
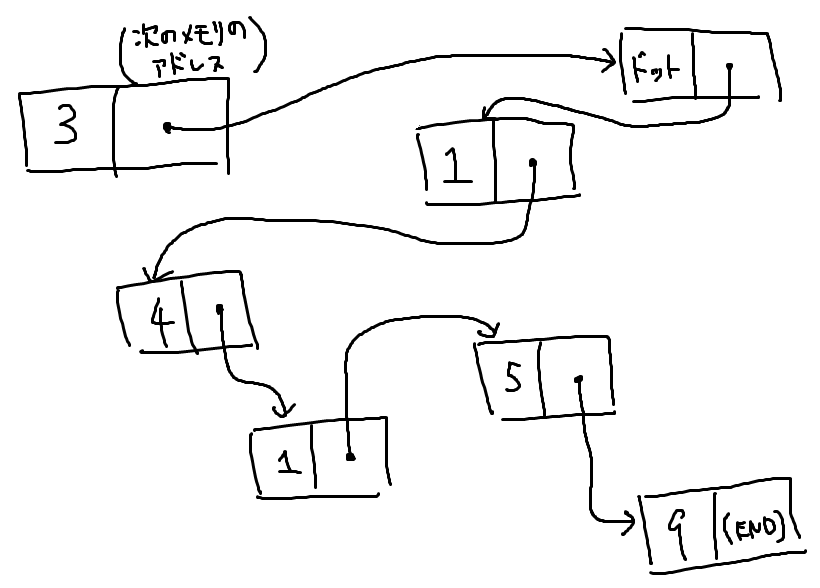
リストのデータの追加は の計算時間・メモリ量でできます。また逆操作をすることで削除も でできます。
一方で、配列とは違いアイテムがメモリ上に一列に並んでいません。
通常のCPUでは残念ながらリスト構造のデータを効率よく調べることが出来ません。リストの長さを とすれば、一番最後のアイテムが何かを調べるためにリストのアイテム全てを辿らないといけないため、 の計算時間がかかってしまいます。
| 実装方法 | 値の読み書き | 値の追加削除 |
|---|---|---|
| 配列 | ||
| リスト |
知ってる人向け: 配列とリストは、アイテムのアクセスとアイテムの追加削除の性能が一長一短となっています。どちらも で処理できる構造というのは(私が知る限り)存在しませんが、 や で処理できる構造は存在します。詳しくは 平衡二分探索木 で調べてみてください。この記事では扱いません。
永続データ構造について
永続データ構造とは、永遠に続くという名のとおり、永遠に使う事が出来るデータ構造のことです。
「永遠に」というのはどういうことか?通常のデータ構造と比較して説明していきます。
通常のデータ構造では、データを変更することが出来ます。データ構造ですからね、データを変更して処理しないと使い物になりません。例えば配列ならi番目の値をvにする、という処理を行うことができます。この時、元のi番目の値はメモリ上から失われます。そう、つまり元の配列というのは永遠に使えておらず、変更が加えられた瞬間に儚くも消えてしまうのです。
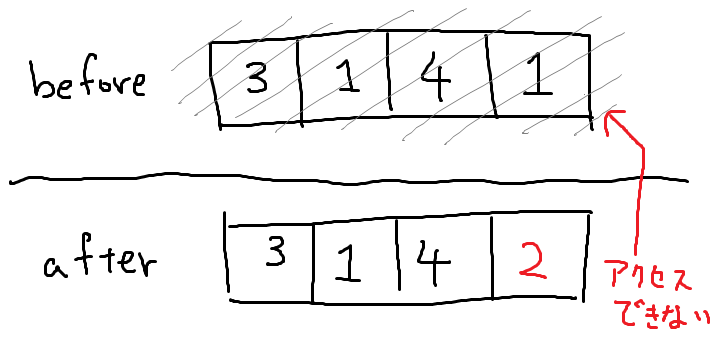
これと比較して永遠に使えるのが永続データ構造となります。すなわち、例えば永続配列ならi番目の値をvに変更する処理を行っても、変更前の配列というものにもアクセスでき、その時のi番目の値を持ってくるということが出来ます。タイムマシンみたいですね。
もちろん変更前の配列に別のデータ変更を加えることで別のバージョンの配列を作り出す、という芸当も可能です(これができる永続データ構造を完全永続データ構造と呼び、出来ない永続データ構造を部分永続データ構造と呼びます)。
今回は永続データ構造の内、永続配列を紹介します。
永続配列
永続配列は次の操作ができるデータ構造です。
- データのアクセス: バージョンと場所を指定し、そのバージョンの配列での値を返す
- データの変更: バージョンと場所と値を指定し、データを変更した新しいバージョンの配列を作成、バージョン番号を返す
ここからは実際に永続配列を実装する方法を3つ紹介します。
配列のコピーによる実装
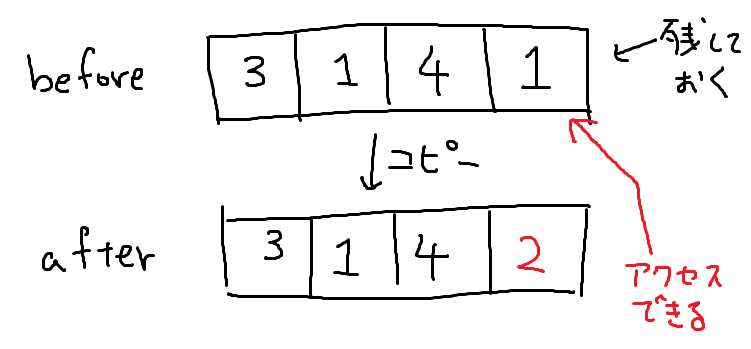
まずは簡単な方法から。元の配列にアクセスできるという構造は、元の配列を残すことで簡単に実現できます。よって、データを変更するたびに配列をコピーしてしまえば、永続配列を実現できます。
データ変更時にかかる計算時間と必要なメモリ量を確認しましょう。一回データを変更するには、配列をどこかにコピーしてあげる必要があるので、それぞれ の計算時間・メモリ量がかかります。
アクセスは です。配列と同じですね。
変更履歴の保持による実装
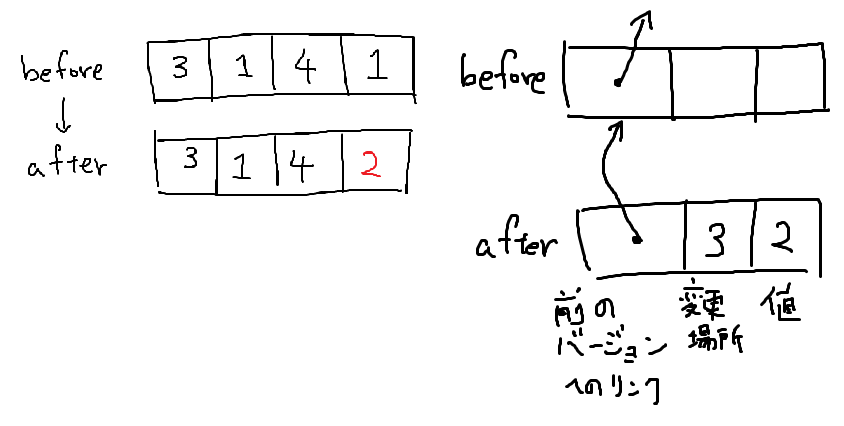
1個値を変更しただけで、N個もの値をコピーしないといけないなんて、割に合わないと思いませんか?そう、変更した部分だけ記録して……
という事を考えてみましょう。バージョン1の配列からi番目の値をvに変更してバージョン2の配列を作るとします。そうしたとき、バージョン2は次の3つの値を持つことで表現ができます。
- 直前のバージョン(今回は1)
- 変更箇所(今回はiとv)
この値は定数個(3個)しかありません。つまりデータを変更するたびに必要な計算時間とメモリは になります。良さそうですね。
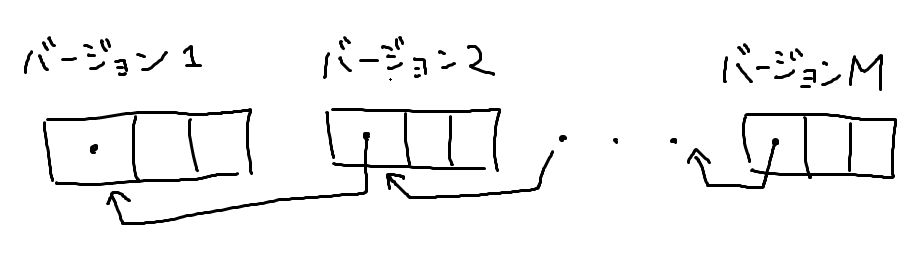
ではアクセスの仕方を考えましょう。バージョンXのi番目の値を知りたいとします。これは次のようなアルゴリズムで解決できます。
- バージョンXでi番目の値が変更されていたら、その時の変更値vを返す。
- そうでなければ、直前のバージョンをYとしてバージョンYのi番目の値を返す。
これを繰り返し、前へ前へと辿っていくと、いずれかは値が変更された箇所か、一番最初の初期配列へと辿り着きます。こうすることで、知りたいバージョンでの値を得られます。
この最悪計算時間はどうなっているかというと、変更回数、つまり最終バージョンをMとすると、最悪なのはバージョンの列が一直線になっていて、値を知るために初期配列まで辿らないといけない場合です。この時の計算時間は です。
変更回数が少ない、何回もデータを読まない、とにかくメモリを少なく済ませたい、という前提なら使えるかもしれませんが、なかなか使いづらいデータ構造になってしまいます。
蛇足: この考え方に、変更履歴で構成された木のEuler Tourと、y-fast trieという2つの構造を組み合わせることで、変更時のメモリ量 かつ変更時・アクセス時の計算時間 を達成する永続配列が存在します(するらしいです)。かなり高度な内容なのでこの記事では扱いません。また、この方法は関数型データ構造でなくなる可能性があります。
完全二分木による実装
今回の記事で紹介したかったアルゴリズムがこちらになります。
先に述べると、データ変更時に必要なメモリ量は 、データ変更時及びデータアクセス時に必要な最悪計算時間は となっています。先に紹介した2つの間のような値になっていますが、対数というのは天文学者の寿命を倍に延ばした実績があるように、実用上は非常に小さく済む値なので、かなり効率が良いアルゴリズムと言えます。
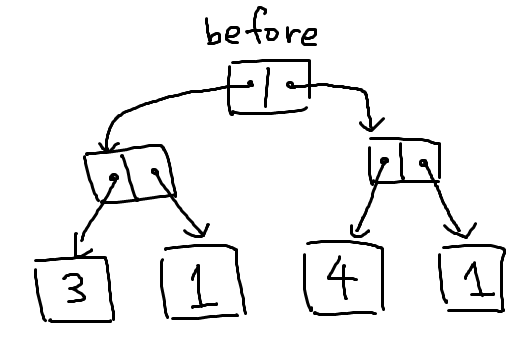
アルゴリズムの概要を示します。まず、一番最初の配列を完全二分木で表現します。今回は という場合でk段の木構造を用意します。
木構造とはグラフ理論における構造の一つで、枝分かれしていく様子が植物の木と似ていることからその名が付けられています。二分木はその分かれ方が2つに分かれるような木で、完全二分木は葉(終点)以外のすべての場所で2つに枝分かれしているものです。
そしてここからがポイントです。
まず、変更前の完全二分木と、変更後の完全二分木を比較してみましょう。
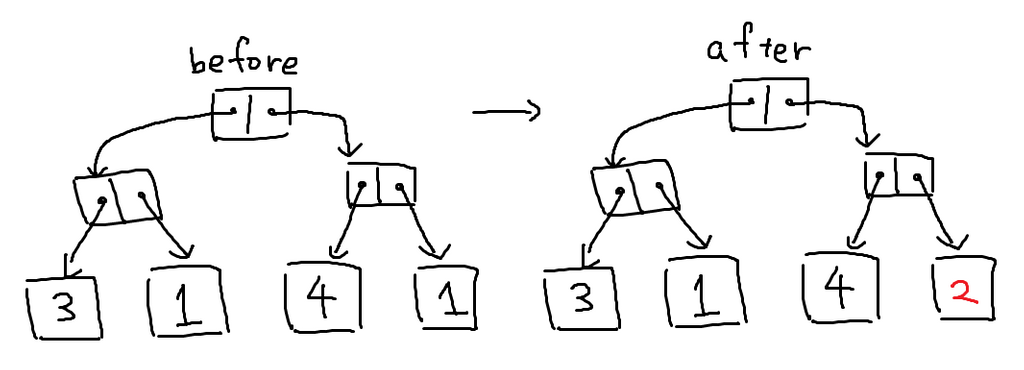
すると、赤く囲った部分は全く変わっていません。
変わっていないというのは、葉ならば入っている値、葉じゃないなら枝分かれした行き先、が変わっていないことを言います。
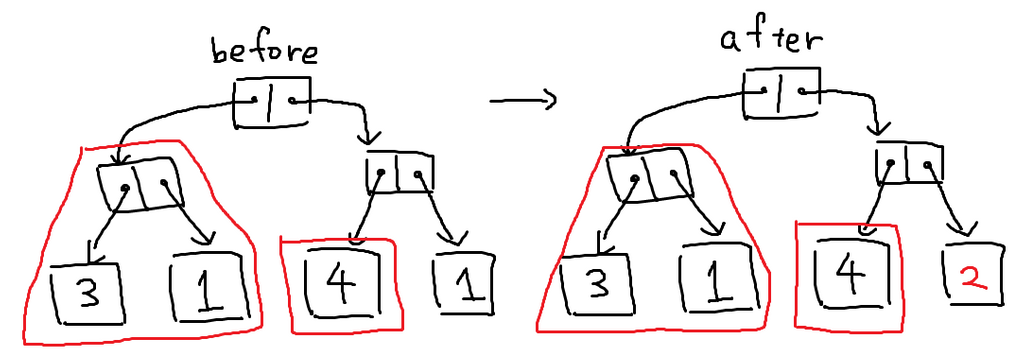
この部分を使い回すことで、新しい完全二分木として作る必要のあるパーツが、木の高さ分だけで済むようになります。
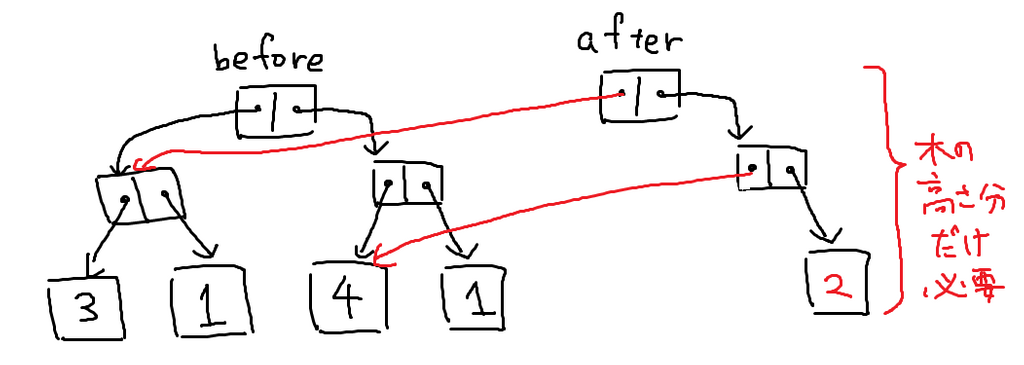
バージョンごとに一番上の部分がどこかを保存しておけば、i番目の値を調べたいときにも木の高さ分だけ辿れば良く、データの読み書きが で済む、という実装になります。
ところで、長さ4の配列をコピーする実装の場合に必要になるメモリ(4個分)と大差ない(5個分)ように見えますが、 のように大きなサイズになった場合、その差は
- 配列のコピー: 個の箱
- 完全二分木: 個の箱
と雲泥の差となります。これは変更履歴の記録による実装に対しても同じような差があります。
| 実装方法 | 値の変更 | 値の読み |
|---|---|---|
| 配列のコピー | ||
| 変更履歴の記録 | ||
| 完全二分木 |
何が嬉しいの?
さて、永続配列を考えることで何が嬉しいのでしょうか?
蛇足: 「嬉しい」は理系の方言らしいですね。どういう動機があるのか、とかそういう意味です。
純粋関数型言語で使える
純粋関数型言語のパラダイムでは、関数は副作用を生まず、変数は代入ができない(語弊がありそう)という参照透過性を保つ必要があります。値を書き換えられないということは、データが破壊されることがまず無いため、扱うデータ構造は基本的に永続データ構造になります。
永続データ構造の中でも、純粋関数型言語で扱える、変数の代入を用いない実装の永続データ構造を純粋関数型データ構造と呼んだりします。今回紹介した永続配列は新しくメモリを確保はしますが、既存の配列に関して代入を行っているわけでは無いため、そのままHaskell等でも実装することができます。多分(実際やったことないので……)。
過去のデータ構造にアクセスできる
永遠に使えるので当然ですが、過去のデータ構造に簡単にアクセスすることができます。
例えば時系列で変化するデータ構造において、ある条件を満たすようになったタイミングを探すために、現在と過去を行ったり来たりして二分探索する、というような用途などに使うことができます。
他にも、データの追加の順番を考えると、最初のデータからある番号までのデータに対するデータ構造、というものにアクセスできます。
競技プログラミングにおいてはこの性質を利用することで、様々なデータ構造を進化させることができます。
競技プログラミングのちょっとした紹介
競技プログラミングについて詳しくは明後日ごろの記事に書かれると思いますが、ここでも軽く紹介します。
競技プログラミングはその名の通りプログラミングで行う競技です。
ネーミングはプログラミング一般に聞こえますが、基本的にはアルゴリズムとデータ構造を問う問題が多く出ます。
この競技プログラミング、競プロは決められた制限時間のあるコンテストでいかに問題を解けるプログラムを早く書けるか、を競うのですが、アルゴリズムの腕試しが出来る他、コンテスト後には解説が公開されるため、そこで新たなアルゴリズムやデータ構造、考え方に出会うことができます。
興味がある人は是非参加してみてください。
おわりに
いかがだったでしょうか?
今回紹介した永続データ構造は、アルゴリズム・データ構造の中でもごくごく狭い分野となっています。
情報科学分野ではこのような面白いパズルのようなアルゴリズム・データ構造がたくさんあります。
興味がある人は、是非情報系の講義を聞いてみたり、競技プログラミングコンテストに参加してみてください。私みたいに「裏側の仕掛けを見たい」というタイプの知識欲がある人はきっとハマりますよ。
明日は Yosotsu さんの記事です。お楽しみに!
