解説 Advent Calendar 2017 - Adventar の14日目の記事として、Advent Calendar Contest 2017 - yukicoder の11日目の問題の解説を書きます。ややこしいですね。どうもnariです。traP Advent Calendar 2017ではありません。

(画像は『フカシギの数え方』 おねえさんといっしょ！ みんなで数えてみよう！ - YouTubeより)

問題ページ : https://yukicoder.me/problems/no/611

問題概要

高さ $H$ 幅 $W$ のグリッド状の盤面がある
各マスには 1~9 の数字か、"?" が書かれている
?のマスは 1~9 のどれかが入る
?のマスが $x$ 個あるとすれば $9^x$ の可能性がある

?のマスを全て1とした時の左上から右下への最短距離を $T$ とする
考えられる盤面の内、左上から右下への最短距離が $T$ になるような盤面の数を数えよ(mod 201712111)

制約

$4HW\le 1211$

入出力例

省略(yukicoderのページに丁寧に書いてあるのでそれを参考にするのがいいです)

考察

制約の確認

$4HW\le 1211$ という、12月11日の問題らしい制約がついています。注目すべきなのはこれが積に対する制約ということです。
整理すると $HW\le 302$ です。これはすなわち $\min (H,W)\le \sqrt{302}<18$ となります。

一般性を失わずに、$H\le W$ だと仮定します。
すると $\min (H,W)=H$ なので、$\min (H,W)$ の上限は $H$ の上限です。
$H\le W$ としているので、$H$ の上限は $W$ です。
よって $H=W$ となるような時が一番 $\min (H,W)$ が大きくなることになります。この時、$HW=H^2\le 302$ なので、$H\le \sqrt{302}$ となります。

積の制約は基本的にこのように値の範囲が特殊になり、これを利用する問題が多いです。
今回だと小さい方の値が18未満となるため、$2^{17}$ とかで通してくださいという作問者の意図を感じ取ることができますね。

$T$ を求めるパート

この問題では右方向か下方向にしか移動しない(つまり遠回りしない)ので、普通にDPが出来ます。
具体的には以下のような更新式で可能です。

dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + (cost[i][j]=='?' ? 1 : cost[i][j]-'0')

問題の整理

ここからどのように盤面を数えるかに入るわけですが、一旦問題を整理しましょう。
$T$ を求めるパートで更新した際に、更新に使った値を持つマスの方向に辺を張ってグラフを構築してみましょう。上も左も同じ値だった場合は両方に辺を張ります。

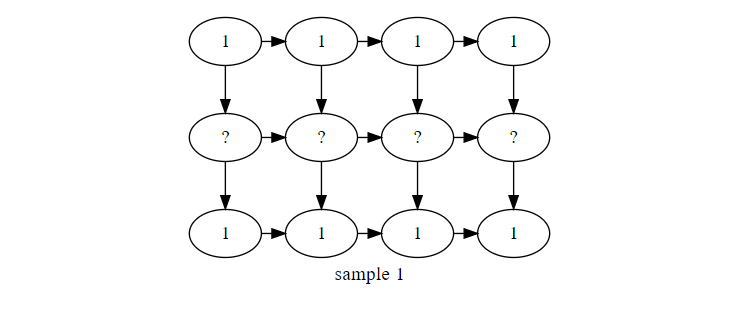
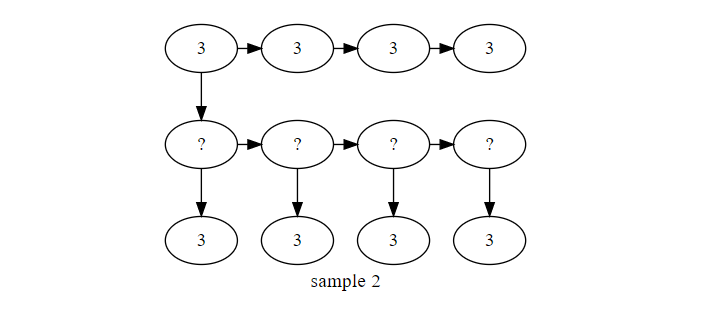
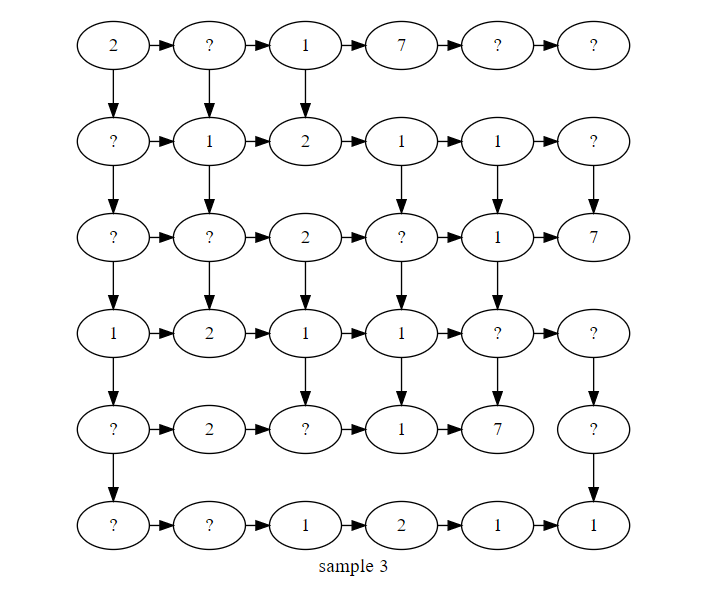
このグラフを辿って右下まで行ければ $T$ 時間が達成できます。ただし、?のマスが1で無い場合は、そのマスが通れないことになります。

2以上だった時の?のマスを通っても $T$ 時間にならないため

つまり問題は次のように言い換えられます。

「グラフ上に?のマスがいくつかある。それぞれ1~9の値を取りうる。?のマスは、値が1の場合のみそのマスを通ることが出来る。考えられるグラフの内、左上から右下に到達できるグラフの数を答えよ。」

ということで到達可能なグラフの数え上げ問題として記述することが出来ました。

解法 : bit DP

この問題はbit DPによって解くことが可能です。具体的なオーダーを先に示すと $O(WH{2}^{\min (W,H)})$ です。空間計算量が $O(WH{2}^{\min (W,H)})$の遷移が $O(1)$ のDPになります。(実際にはテーブルを使いまわして空間計算量は $O(2^{\min (W,H)})$ にしないと大変そう)
状態は「今どのマスを見ているか($WH$通り)」「前一行のマスの(1,1)との接続状況($2^{\min (W,H)}$通り)」を持ちます。
なぜこの状態数で大丈夫かというと、「左上から右下にパスを繋げる」というのを数え上げる際に、今着目しているマスの一つ上の行以外のマスが(1,1)と繋がっているかというのはどうでも良いからです。

具体的な例を見てみましょう。サンプル1のグラフで、現在(2,3)のマス(上から数えて2、左から数えて3)に着目しているとします。

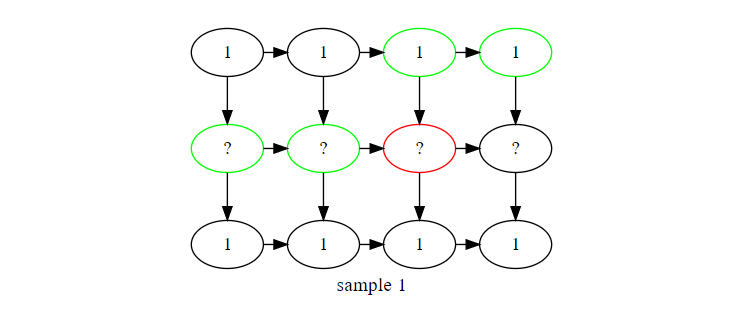
赤いマスが現在着目しているマス、緑のマスがDPの状態として保持するマスです。DPの更新では、赤いマスが(1,1)から到達可能か？というのを調べる必要があります。
この更新は簡単です。上のマスからの辺があれば上のマスの到達可能性を調べ、左のマスからの辺があれば左のマスの到達可能性を調べ、どちらかが成り立っていれば到達可能、そうでなければ到達不可能、として、次の状態に遷移すればOKです。
ただし現在着目しているマスが"?"のマスであれば、9通り試す必要があります。もしも1であれば上述した到達可能判定をすれば良いですが、そうでなければそのマスは通れないことにしていましたから、問答無用で到達不可能とします。

次の図のような到達可能性状況であれば、

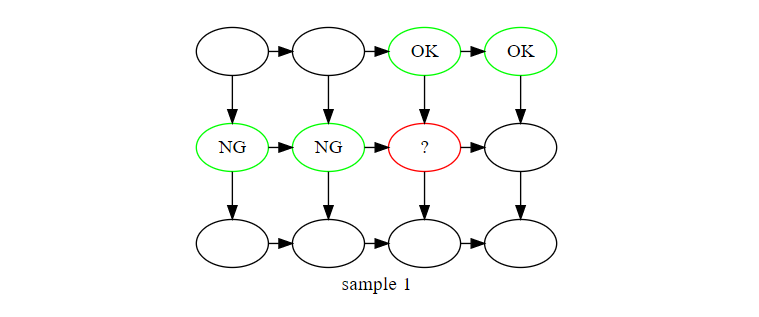
このように更新されます。

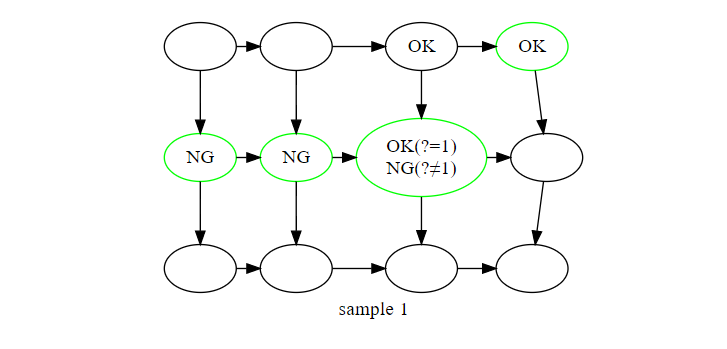
このDPを、着目するマスを(1,1)→(1,2)→...→(1,W)→(2,1)→... というように、左から右、右端に行ったら一行下がってまた左から右、という順番で行います。この時、行のサイズが$W=\min (W,H)$となっていれば保持するべき「一つ前の行の到達可能性」というのは$2^{\min (W,H)}$に抑えられます。
$H=\min (W,H)$の場合は逆にすれば良いですが、グラフを対角線で反転させて対処するとコードを書く量が減ります。

これでこの問題は解けました。

終わり。

このタイプのDP

このタイプのDPは指数時間アルゴリズム入門という有名なスライドにも実は紹介されていて、17ページから書かれている「幅を活用した動的計画法」というのがそれです。なかなか見ない問題ですけどね……

フカシギの数え方

みなさんはこの動画はご存知ですか？僕はご存知です。

簡単に説明すると、グリッドの最短経路を通るようなパスの数え上げというのは組み合わせで記述できますが、最短経路でなくとも良いようなパスの数え上げは組合せ爆発して全探索が出来ない、という問題です。「自己回避歩行(Self-Avoiding Walk)」という名前がついていたりします。

これを解くアルゴリズムも実は今回のアルゴリズム同様に幅を活用した動的計画法で解けてしまいます。
『フカシギの数え方』を解説した書籍、超高速グラフ列挙アルゴリズム 〈フカシギの数え方〉が拓く，組合せ問題への新アプローチ | 森北出版株式会社 ではフロンティア法という名前で紹介されています。ZDDというなんかすごそうな名前の付いたデータ構造を用いて計算していますが、通り数を数えるだけであれば単純な動的計画法だけで解けます。
フロンティア、というのは先程のアルゴリズムで言うと「一行前」の部分を指しています。かっこいいですね。
詳しい解説は書籍を読んで下さいという感じですが、軽くアルゴリズムを紹介します。

問題概要

グリッド上の無向グラフで、左上から右下までの単純パスを数え上げる、という問題。

考察

グラフの特徴を数学的に記述すると次のような特徴があります。

• 始点と終点の次数は1
• それ以外の頂点の次数は2か0
• 閉路が無い

これを満たすグラフは全て条件を満たします。

状態

11日目の問題同様、一行前の接続状況(フロンティア)を状態として持ちます。
次のような状態を持ちます。

• 始点と繋がっているか
• 次数1の頂点で、フロンティア内のある頂点とある頂点が繋がっているか
  • すでに次数が2の頂点の接続状況は無視して良い

遷移

遷移は次のようなものになります。

• 今着目している頂点を次数1の頂点1つとつなぐ
  • 元の頂点の次数が2になり、新しく次数1の頂点がフロンティアに出来る
  • 接続状況も更新する
• 今着目している頂点を次数1の頂点2つとつなぐ
  • この時、もともとつながっていた次数1の頂点2つをくっつけると閉路が出来てしまう
  • なので、違う連結成分になっている頂点しか繋げない
  • もともと次数1だった頂点2つは次数が2になり、今見てる頂点も次数が2になる
• 今着目している頂点を次数1の頂点にする
  • ちょっと複雑
  • 着目する頂点の進め方によるけど、ある辺を使って、その端点を次数1とする
  • 片方はフロンティアに残る必要がある
• 何も繋がない
• ただし各遷移において、フロンティア外に始点以外の次数1の頂点を残してはいけない
  • なので、着目してる頂点の上に次数1の頂点があった場合は基本的に繋ぐことになります

ちょっと複雑ですが、意外と簡単に見えませんか？
ちなみに一般的なグラフでも(幅が小さければ)使えます。またグリッドグラフの中に障害物があって通れないような場合でも問題なく数え上げられます。
みんなもおねえさんを救おうね。

類題

実は11日目の問題を見た時にすぐにフロンティア法だなぁと思っていました、というのは私が競プロに没頭してすぐにフロンティア法にあたって、割と印象に残っていたからです。
その問題というのがSRM671のHard、BearDestroysというものです。およそ2年前ですね。
この問題は当時全く解けなかったのですが、解説を読んだ時に、$2^W$ とか $2^H$ とかいう計算量を見て「何だこれは……まるで意味が分からんぞ……」と思った記憶があります(当時はbit DPもあまり知らなかったので)。
その後無限に考えてようやく理解したということがあったので、とても思い出深い問題です。
この問題はグラフというよりは単純なbit DPなのでおねえさんの問題よりかは解きやすいと思います。ぜひ解いてみてください。

おわりに

ところで自己回避歩行を課題に出してきた講義があるんですよ。東京工業大学の情報実験第一って言うんですよ。
その講義、30000頂点の巡回セールスマン問題も課題に出してきたんですよね。やばいですね。