こんばんは。nariです。この記事は「解説 Advent Calendar 2017」の6日目の記事です。traP Advent Calendar 2017ではありません。

(画像は「いらすとや」より「険しい道のりのイラスト」です)

JAG模擬地区予選オンサイトに参加するつもりでしたが、がっつり風邪をひいて参加できなかったので、一昨日と昨日でチームで一通り解いてみました。(AtCoder Virtual Contest)
今回はその中で考察が面白かったD問題 - Revenge of the Broken Door - の解説を書いてみます。

コンテストリンク / 問題リンク

問題概要

若干ゃ意訳です。

$N$ 頂点 $M$ 辺の単純連結無向グラフが与えられます。各辺にはコスト $c_i$ がついています。
頂点 $S$ から頂点 $T$ へ移動したいのですが、辺のうちある1本だけが通行止めになっています。この通行止めになっている辺は辺を通ろうとした時、つまり辺のどちらかの端点に到着した段階で知ることができます。それまではどの辺が通行止めかわかりません。
このような状況で $S$ から $T$ へ移動する戦略を考えた時、実際に通行止めだった辺によって最悪かかってしまう時間を最小にする戦略の最悪時間を求めてください。
通行止めの辺によっては $S$ から $T$ へ移動できない場合があります。このような場合は-1を出力してください。

制約

$1\le N\le 10^5$
$1\le M\le 2\times 10^5$
$S\ne T$

入出力例

1

入力

3 3 1 3
1 2 1
2 3 5
1 3 3

グラフ

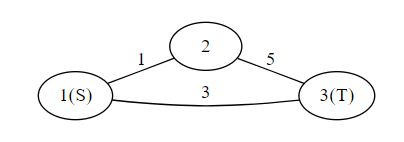
出力

6

詳細

「1→3が通れるならそれ、そうじゃないなら1→2→3」という戦略を考えると、前者は3、後者は6で通れるので、最悪時間は6です。

「1→2→3が通れるならそれ、そうじゃないなら1まで戻って1→3」という戦略の場合、2→3が通れないと分かるのは2に着いた時なので2→3が通行止めの場合の時間は5になります。ただしこの場合1→2→3が通れた場合の時間が6なので、最悪時間は6です。

2

入力

4 4 1 4
1 2 1
2 4 1
1 3 1
3 4 1

グラフ

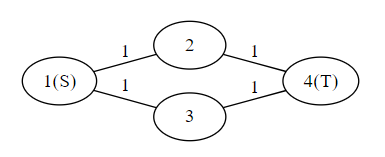
出力

4

詳細

「1→2→3をトライする」戦略の場合の最悪時間は、2→3が通行止めだった場合で、1→2→1→3→4のようなルートになるので4になります。
これは「1→3→4をトライする」戦略も同様です。

3

入力

5 4 4 1
1 2 3
2 3 4
3 4 5
4 5 6

グラフ

出力

-1

詳細

一本道なのでどこかの辺が通行止めになると完全に分断されます。

考察

問題の整理

最悪のケースとか曖昧なので、まずはちゃんと定式化しましょう。
「戦略」のうち考えれば良いのは結局どのパスを通ろうとするかだけで十分です。最悪時間の候補は、パスのどの辺も通行止めでなくストレートに行けた場合と、どこかの辺が通行止めで、その辺の端点から $T$ へのその辺を除いた最短経路を通る場合のどれかです。

考えるパス(長さ $L$ )を $p_1(=S),p_2,\dots ,p_L(=T)$ とします。その時の最悪時間は以下の式で書けます。
$worst(p)=\max \left(len(p),\underset{1\le i\le L-1}{\max }\left(len(p_{1,2,\dots ,i})+dist2(p_i,p_{i+1})\right)\right)$
ただし $len(p)$ はパスの長さ、$dist2(p,q)$ は $p$ から $T$ への辺 $(p,q)$ を用いない最短距離を表します。$dist2(p,q)$ に関して $T$ へ到達不能の場合は $\infty$ を返すことにします。

よって求める解は $ans={\min }_{p}worst(p)$ と書けることになります。

解の二分探索

「最大値の最小値」を求める場合、解に関して二分探索して値を固定してしまうことで問題が簡単になることが多いです。今回もそうします。
解がある値 $X$ 以下だとします。すると、$worst(p)\le X$ なるパス $p$ が存在することになります。
もうちょい書き下すと $(len(p)\le X)\wedge \left(\forall i,len(p_{1,2,\dots ,i})+dist2(p_i,p_{i+1})\le X\right)$ です。$X$ を固定したことによって面倒だった $\max$ が消えて条件に変わって扱いやすくなりました。
このようなパスが存在するかどうかはdijkstra法を少し書き換えれば簡単に判定可能です。距離を保存・更新するのはdijkstra法同様で、枝を使って更新する際に先程の $X$ に関する条件を満たす場合のみ更新する、という形にすれば良いです。

この時点での時間計算量は、$dist2(p,q)$ が $O(1)$ でアクセス出来るとすれば $O((N+M)\log N\log \max (ans))$ です。$ans$ は適当に見積もっても高々 $2M{\max }_i{c}_i$ ぐらいなので十分高速ですね。

dist2の問題整理

残る問題は $dist2(p,q)$ です。これさえ計算すれば前述の計算量で元の問題が解けます。
ということで $dist2(p,q)$ の性質を考えます。

まず、任意の地点から $T$ への最短路、というのは高速に計算できないので、$T$ から任意の地点への最短路を計算することを考えます。こちらは通常のdijkstra法で容易に計算できます。
任意の地点 $p$ から $T$ への最短距離を $dist(p)$ とします。またdijkstra法で使った辺のみで構成される木を最短路木と呼びます。

$(p,q)$ が最短路木に含まれない場合、$dist2(p,q)=dist(p)$ です。問題は $(p,q)$ が最短路木に含まれる場合の計算です。

例として、入力例2の最短路木は次の図のようになります。赤い辺は最短路木に含まれない辺です。

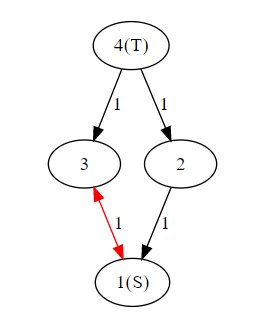
例えば $dist2(2,4)$ を考えるとします。$(2,4)$ は最短路木に含まれています。

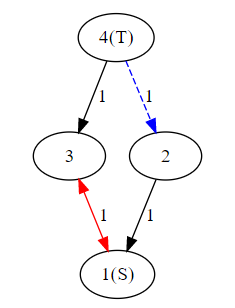
この場合、$dist2(2,4)$ は3になります。最短路木の辺を一本削除して、木においては頂点2と $T$ が分離しているので、例のように必ず最短路木に含まれていない辺を1本使うことになります。
つまり、下式で表せることになります。

$dist2(p,q)=\underset{x\in subtree(p)\wedge y\notin subtree(p)\wedge (x,y)\in E\setminus minpathtree}{\min }dist(x)-dist(p)+cost(x,y)+dist(y)$

ただし $subtree(p)$ は最短路木の点 $p$ を根とした部分木の頂点集合を指し、$minpathtree$ は最短路木の枝集合を指します。
これは $p$ から $x$ まで最短路木の辺を使って移動し、$(x,y)$ を使って最短路木の $T$ を含む連結成分へ移動、後は最短路木を辿って $T$ まで移動、というものを表しています。
例では $p=2,x=1,y=3$ となっています。

一応これで $(p,q)$ を用いない最短経路になっていることを軽く示すと、まず前述したとおり最短路木に含まれない辺を1本も使わない場合はそもそも $T$ へのパスが作れません。
1本使う場合は、分断された木を繋ぐ必要があるので、上式に表されたとおりになります。
2本以上使う場合は考える必要がありません。必要な1本を除けば他の移動は最短路木を辿れば最短であることがわかっているためです。

オイラーツアーとRMQ

少し書き直すと先程の式は次のようになります。

$dist2(p,q)=\underset{x\in subtree(p)}{\min }\left\{dist(x)+\underset{y\notin subtree(p)\wedge (x,y)\in E\setminus minpathtree}{\min }(cost(x,y)+dist(y))\right\}-dist(p)$

部分木に関する $\min$ が出てきたので、オイラーツアーとRMQの組み合わせを思いつきます。

また、$dist2(p,q)$ の計算を最短路木の根からトポロジカル順序で処理していくことを考えると、最短路木に含まれない辺 $(x,y)$ を使えるようになるタイミングは $p=lca(x,y)$ の $dist2(p,q)$ が計算し終わった後です。
これは $(x,y)$ が計算に影響をあたえるのはそれらを含む部分木のみであること、そしてそれを使えるようになるタイミングというのは $x,y$ が今後ずっと別の連結成分に属するような瞬間であることからわかります。

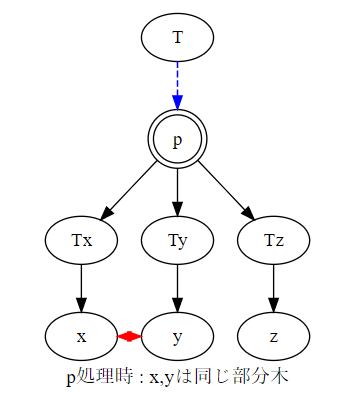
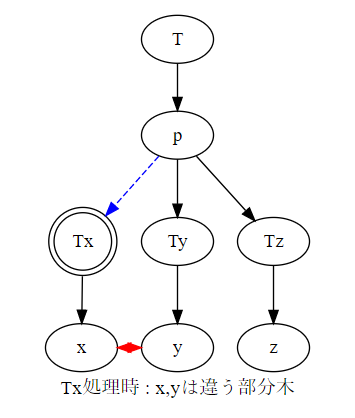
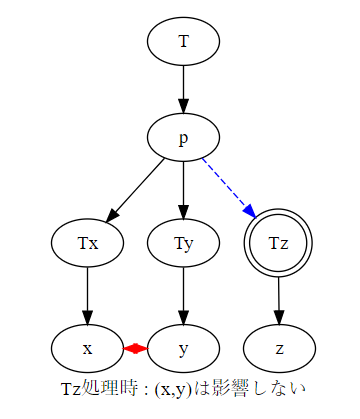
よって、以上を合わせると次のようなアルゴリズムが思いつきます。

1. 最短路木に含まれない全ての辺についてLCAを計算してその頂点の処理リストに追加する
2. 最短路木の根からトポロジカル順序で以下の処理をしていく
   1. 現在のRMQを使って $dist2(p,q)$ を計算する
   2. $p$ の処理リストの辺を使ってRMQを更新する

LCA/RMQとしてsegment treeを用いれば、時間計算量は $O((N+M)\log N)$ を達成します。

以上で元の問題が解けました。

まとめ

まとめると、問題を整理して、解を二分探索して、dijkstra書き換えて、もう一回問題を整理して、最短路木作って、LCA計算して、オイラーツアー作って、順番にRMQを更新すると、解けます。大変ですね。
でも一つ一つはそこまで難しくない気がしますね。私は今回は自力で解けましたがICPC本番だと時間を使ってしまいそうだしそもそも解ける自信が無いですね……

考察するとどんどん問題が小さくなっていくとても面白い問題でした。他にもJAG模擬地区予選は面白い問題がいっぱいあったのでぜひ解いてみてください。JAGの皆さん面白い問題をありがとうございました。来年はちゃんとオンサイト行きます。

解説Advent Calendarということで解説を書きましたが、真面目に解説書くの慣れてないのでもしかしたら不備があるかもしれません、何かあったらコメントしていただくか @_n_ari にリプライください。よろしくお願いします。