【衝撃】円周率を小数点以下100万桁まで知る方法4選【分割統治FFTあり】

この記事は、アドベントカレンダー2025の19日目の記事です。

はじめに

お久しぶりでございます。Naru820です。~~ついにネタがなくなったので真面目？な記事を書かざるを得なくなりました。無念。~~

突然ですが、皆様は円周率をご存じでしょうか？おそらく小学校で習った上に、テレビやYoutubeなどで円周率を暗唱するシーンがちょくちょく出てくるので、名前ぐらいは知っているかと思います。ちなみに僕は3.14159265358979...ぐらいしか覚えていません。これでは突然円周率バトルを仕掛けられたときに勝てませんね。

ということで、今回は円周率バトルの対策に、円周率を小数点以下100万桁まで知る方法を厳選して4つご紹介します。

本文

御託はここまでにして早速見ていきましょう。なお、以下では円周率を略してπと呼ぶことがあります。

インターネットを検索する

皆様が今このブログを閲覧しているであろうブラウザの検索欄に、「π　小数点以下100万桁」と打ち込んで検索すると、複数ヒットすると思います。そのサイトにアクセスすればいいです。よって、目的を達成することができます。

同人誌を買う

円周率が小数点以下100万桁が書いてある同人誌があるので、これを買えばいいです。一つ前の方法と比べると、手間もお金もかかりますが、これでも目的を達成することができます。

自分で計算する

ご存じの方も多いかと思いますが、πは数学の至る所に登場します。円や球を考えるときには登場するのはもちろんのこと、一見円や球とは全く関係がなさそうな分野にも、唐突に登場します。

非常に有名なものとしては、 $ζ (2) = n = 1 \sum \infty \frac{1}{n ^{2}} = \frac{π ^{2}}{6}$ (バーゼル級数とも呼ばれます)であったり、ガウス積分 $\int_{- \infty}^{\infty} e^{- x^{2}} d x = π$ などがあげられるでしょう。
他にも初等的に結果が示せるもので有名なものは、ウォリス積であったりビュフォンの針などまだまだたくさんあり、πが登場する数式には枚挙にいとまがありません。

このように、いろいろな数式にπは登場します。ということは、逆に考えると、その数式の(近似)値を別の方法で計算してしまえば、πの(近似)値が求まることになります。

今回近似計算に使用する級数は、以下のChudnovskyの公式と呼ばれているものです。(証明は省きますが調べたら出てきます。)

$\frac{1}{π} = \frac{12}{C ^{\frac{3}{2}}} n = 0 \sum \infty \frac{( - 1 ) ^{n} ( 6 n )! ( A + B n )}{( 3 n )! ( n ! ) ^{3} C ^{3 n}}$ (ただし、 $(A, B, C) = (13591409, 545140134, 640320)$ )

この公式の右辺の級数の部分和を計算すれば、πの近似値を求めることができます。明らかに登場している数字がデカすぎるんですが、そのデカさに見合ったいいところがありまして、この公式は収束するのが非常に速いことが知られています。分子と分母を見比べると明らかにn項目が爆速で0に行くのは目に見えていますからね。具体的には、1項計算するごとに精度が大体14桁ずつ上がっていきます。簡単に証明しておこうと思います。

証明

$a_{n} = \frac{12 ( 6 n )! ( A + B n )}{( 3 n )! ( n ! ) ^{3} C ^{3 n + \frac{3}{2}}}, S_{n} = k = 0 \sum n (- 1)^{k} a_{k}, E_{n} = \frac{1}{π} - S_{n}, S = \frac{1}{π}$ とします。定理の主張は $n \to \infty lim S_{n} = S$ と書けます。
( $S_{n}$ が絶対収束することは認めます。ダランベールテストをすればすぐにわかります。)

まず補題を2つ示しておきます。

補題1

任意の非負整数 $n$ に対して、 $E_{n} < a_{n + 1} .$

証明(補題1)

任意の非負整数 $n$ に対して、 $a_{n + 1} < a_{n}$ が成り立ちます。(これは面倒なだけで計算すればすぐにわかるので証明は省きます。)

以下を示すことができます。

$S_{2 n} > S$
$S_{2 n + 1} < S$

前者について、 $S_{2 n} - S = \sum_{k = n}^{\infty} (a_{2 k + 1} - a_{2 k + 2}) > 0$ です。(絶対収束するため和の順序交換が許されます。) 後者もほとんど同様です。

よって、任意の $n$ について、数直線上での移動を考えると $∣ S_{n} - S ∣ < ∣ S_{n + 1} - S_{n} ∣$ が成り立ちます。(偶奇の場合分けをしてもよいです。)
左辺は $E_{n}$ 、右辺は $a_{n + 1}$ に等しいですから、 $E_{n} < a_{n + 1}$ です。よって示されました。(証明終わり)

補題2

任意の正の整数 $n$ に対して、 $a_{n} < \frac{6 ( A + B )}{( C π ) ^{1.5}} (\frac{1728}{C ^{3}})^{n} .$

証明(補題2)

スターリングの不等式 $2 πn \frac{n ^{n}}{e ^{n}} exp (\frac{1}{12 n + 1}) < n! < 2 πn \frac{n ^{n}}{e ^{n}} exp (\frac{1}{12 n})$ を用います。(証明は省きます。)
これを $a_{n}$ の定義式に用いて整理すると、 $a_{n} < \frac{6 ( A + B n ) 172 8 ^{n}}{( π C n ) ^{\frac{3}{2}} C ^{3 n}} < \frac{6 ( A + B )}{( C π ) ^{1.5}} (\frac{1728}{C ^{3}})^{n}$ が成り立ちます。(証明終わり)
(計算してみるとわかりますが相当雑に評価しています。が、 $C$ が大きすぎて誤差レベルです)

証明続き(元の問題)

さて、 $π$ を $\frac{1}{S _{n}}$ で近似することにしましょう。この誤差は、 $n$ が偶数の時、 $\frac{1}{S} - \frac{1}{S _{n}} = \frac{S - S _{n}}{S S _{n}} = \frac{π E _{n}}{S _{n}} < π^{2} a_{n + 1}$ となります。(補題とその証明で登場した式を使いました。)

よって、 $π$ を小数点以下 $N$ 桁まで正確に計算したいときは、 $π^{2} a_{n + 1} < \frac{6 ( A + B ) π}{C ^{1.5}} (\frac{1728}{C ^{3}})^{n + 1} < 1 0^{- N}$ を満たす偶数 $n$ に対して、 $S_{n}$ を計算すればいいことになります。(厳密にはこれだと確定しないです。例えば、真の値が0が続く場所があったとして、そこから少しずれたら99999のようになるためです。)

両辺に常用対数をとり、整理すると、 $K = lo g_{10} (\frac{6 ( A + B ) π}{C ^{1.5}}), D = - lo g_{10} (\frac{1728}{C ^{3}}) = lo g_{10} (\frac{C ^{3}}{1728})$ として、 $n > \frac{N + K}{D} - 1$ となります。なお、実際には $D \approx 14.181647462825..., K \approx 1.064333...$ です。より粗い評価をすると、 $n \geq \frac{N}{14}$ となります。よって冒頭の14桁ずつ精度が増えていく、ということが示せました。(証明終わり)

(厳密には、 $π$ の値を $K$ の計算で使ってしまっていますが、まあ $3 < π < 4$ は非常に容易に示せますから、気になる人はそうしてもよいです.)

実際に $S_{n}$ を計算する

では、実際に $S_{n}$ を計算するにはどうすればいいでしょうか？

今回は、Binary Splitting Methodと呼ばれる、有理数係数一般化超幾何級数の部分和を高速に計算することが出来るアルゴリズムを使います。(もうちょっと適用範囲は広いですが)分類としては分割統治法の一種です。

一般化超幾何級数とは、以下の形で表される級数の事です。

_{r} F_{s} (a_{1}, \dots, a_{r}; b_{1}, \dots, b_{s}; z) = n = 0 \sum \infty \frac{( a _{1} ) _{n} \dots ( a _{r} ) _{n}}{( b _{1} ) _{n} \dots ( b _{s} ) _{n}} \frac{z ^{n}}{n !}

ただし、 $(a)_{n} = k = 0 \prod n - 1 (a + k)$ はボッホハマー記号です。

一般的な関数の多くは、超幾何級数を用いて表現できることが知られています。(今回はアルゴリズムのほうに主眼を置きたいのでここは深くは解説しません。)

今回の級数も、 $\frac{12 A}{C ^{\frac{3}{2}}}_{4} F_{3} (\frac{1}{6}, \frac{1}{2}, \frac{5}{6}, \frac{A}{B} + 1; 1, 1, \frac{A}{B}; - \frac{1728}{C ^{3}})$ のように表現できます。

Binary Splitting Methodは以下のようなアルゴリズムです。以下では、 $X_{n} = \frac{( a _{1} ) _{n} \dots ( a _{r} ) _{n}}{( b _{1} ) _{n} \dots ( b _{s} ) _{n}} \frac{z ^{n}}{n !}$ とします。

ステップ1

$z = \frac{P}{Q}, a_{i} = \frac{p _{i}}{q _{i}}, b_{i} = \frac{u _{i}}{v _{i}}$ とします。

$S (n) = P (i = 1 \prod r p_{i} + n q_{i}) j = 1 \prod s v_{j}, T (n) = (n + 1) Q (j = 1 \prod s (u_{j} + n v_{j})) (i = 1 \prod r q_{i})$ とします。(このように定義すると、 $\frac{X _{n + 1}}{X _{n}} = \frac{S ( n )}{T ( n )}$ が成り立ちます。)

ステップ2

再帰関数を定義します。 $f (L, R)$ を、区間 $[L, R)$ について、以下の3つの値 $S_{L, R}, T_{L, R}, U_{L, R}$ を計算する関数と定めます。

$S_{L, R} = k = L \prod R - 1 S (k), T_{L, R} = k = L \prod R - 1 T (k), U_{L, R} = k = L \sum R - 1 i = L \prod k S (i) j = k + 1 \prod R - 1 T (j)$

これを分割統治で計算します。 $R - L = 1$ の時は、 $S_{L, L + 1}, T_{L, L + 1}$ は定義通り計算すればいいです。 $U_{L, L + 1}$ も、定義を考えると $S (L)$ に等しいです。

$R - L > 1$ の時、 $m = ⌊ \frac{L + R}{2} ⌋$ として、 $f (L, m), f (m, R)$ を呼びます。そして、

$S_{L, R} = S_{L, m} S_{m, R}$
$T_{L, R} = T_{L, m} T_{m, R}$
$U_{L, R} = U_{L, m} T_{m, R} + S_{L, m} U_{m, R}$

を返します。(これが成り立つことは簡単な通分の計算でわかります。)

ステップ3

$f (0, N)$ を呼んで、 $T_{0, N}, U_{0, N}$ を計算します。 $U_{0, N} = k = 0 \sum N - 1 i = 0 \prod k S (i) j = k + 1 \prod N - 1 T (j)$ ですから、 $\frac{U _{0, N}}{T _{0, N}} = i = 0 \sum N - 1 j = 0 \prod i \frac{S ( j )}{T ( j )} = i = 0 \sum N - 1 \frac{X _{i + 1}}{X _{0}} = i = 1 \sum N X_{i}$ が成り立ちます。

よって、和を計算することが出来ました。(最後に $X_{0} = 1$ を足す必要があります。)

上ではかなり形式的に定義しましたが、意味としては、 $T$ が全体の和を通分した分母(約分はしていません)、 $U$ が全体の和を通分した分子、 $S$ が分子の変化率のようなものです。

時間計算量は、分割統治法のいつもの議論をすると、 $N$ 項の部分和を計算する時、 $O (M (N lo g N) lo g N)$ となります。(ここで、 $M (b)$ は $b$ 桁の乗算にかかる計算量で、現在 FFTにより、 $M (b) = O (b lo g b)$ であることが知られているので、これはおおよそ $O (N (lo g N)^{3})$ です。)

実際にπの近似値を求めるコードの例としては以下のような感じになります。(アルゴリズムのわかりやすさを重視したコードなので、高速化の余地が多々あります。あと多倍長整数演算だけで本当は済ませるべきですが面倒だったので浮動小数点を使用しています。また、直接πを求めるように、分子と分母を入れ替えています。)

import sys
from decimal import Decimal, getcontext
sys.set_int_max_str_digits(0)
getcontext().prec = 1050000
getcontext().Emax = 20000000
getcontext().Emin = -20000000

N = 75000 ## 1000000//14 より大きい整数
A = 13591409
B = 545140134
C = 640320

def s(n):
    return -24 * (6*n + 1) * (2*n + 1) * (6*n + 5) * (A + B*(n + 1))
def t(n):
    return (C**3) * ((n + 1)**3) * (A + n*B)
def compute_pi():
    def bs(L, R):
        if R - L == 1:
            s_val = s(L)
            t_val = t(L)
            return s_val, t_val, s_val
        else:
            m = (L + R) // 2
            s_left, t_left, u_left = bs(L, m)
            s_right, t_right, u_right = bs(m, R)
            return s_left * s_right, t_left * t_right, u_left * t_right + s_left * u_right

    _, T, U = bs(0, N)
    numerator = Decimal(C) * Decimal(C).sqrt() * Decimal(T)
    denominator = Decimal(12) * Decimal(A) * Decimal(T + U)
    return numerator / denominator

pi_val = compute_pi()
pi_str = str(pi_val)
print(pi_str)

このプログラムを実行すると、4,5分ぐらいで計算が終わりました。(ゲームをしていたらいつの間にか終わっていたので正確な時間は測っていません。)また、計算結果を、ネットからダウンロードした円周率1000000桁と比べると一致しました。よって、これでも目的を達成することが出来ます。

y-cruncherを使う

y-cruncherというソフトがあります。ここからダウンロードすることが出来ます。簡単に説明すると、マルチスレッドに対応した計算プログラムです。今年の12月11日に、円周率が314兆桁計算されたというニュースがありましたが、この計算にも使われています。ちなみに、使用しているアルゴリズムや、公式は先程紹介したChudnovskyの公式とBinary Splitting Methodです。

ダウンロードして起動すると以下のような画面になります。

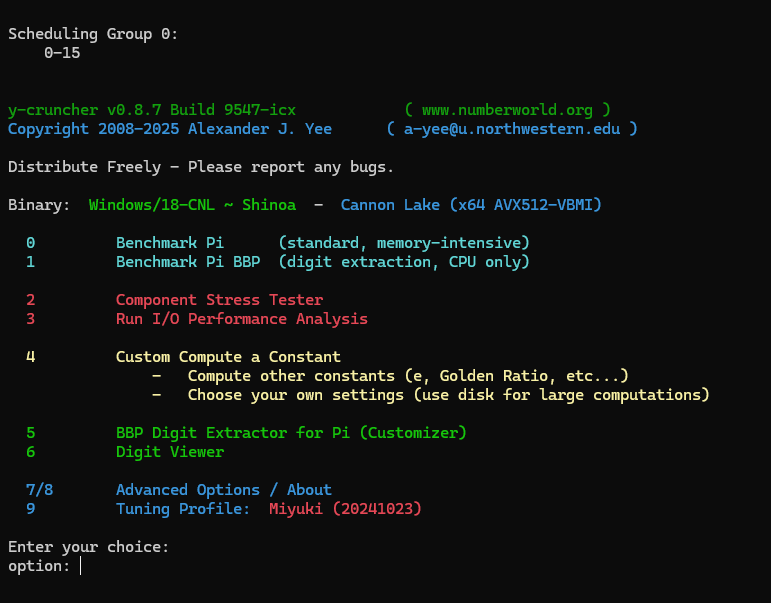
0を選びます。

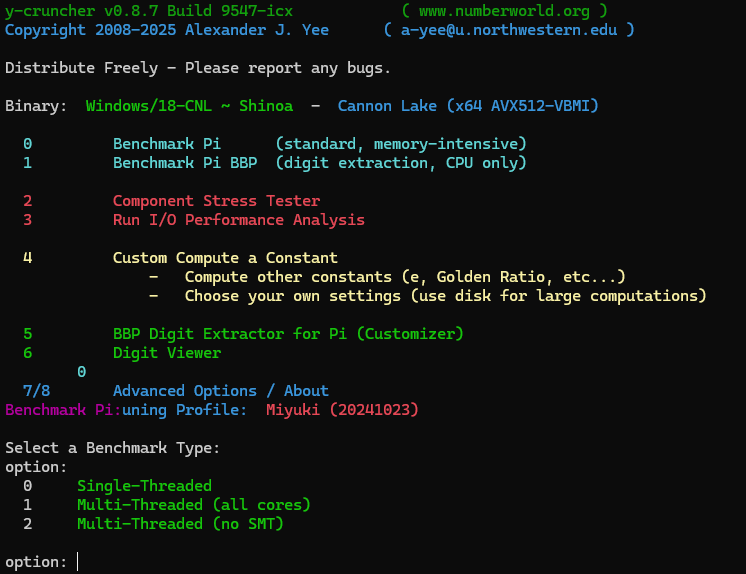
とりあえず1を選びます。

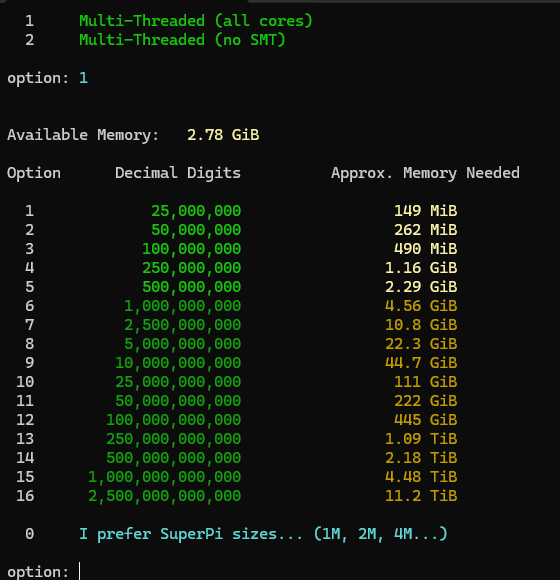
とりあえず0を選びます。

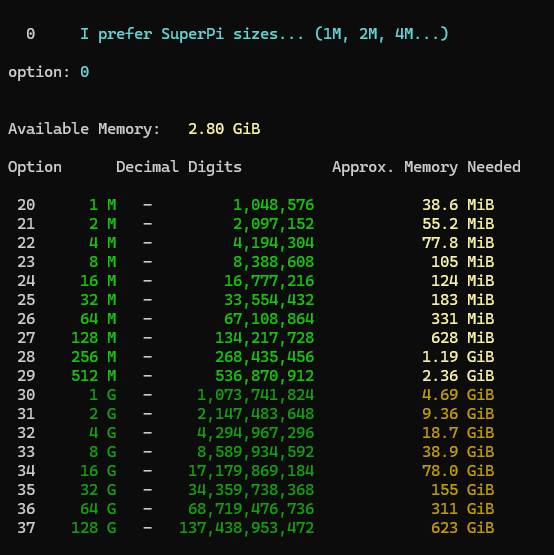
20を選びます。そうすると、以下のような画面が出てきます。

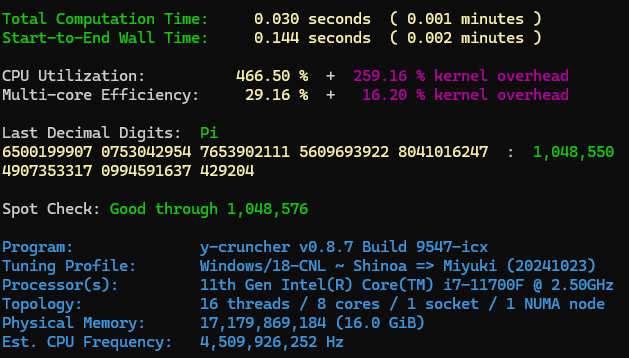
下のほうにそれっぽいテキストファイルの名前が書いてあるのでそれを開くとπの値が指定した桁数計算されているのがわかります。よって、これでも目的を達成することが出来ます。

おわりに

いかがでしたでしょうか？おすすめは最初と最後に述べた方法です。もっと詳しく円周率や他の数学定数の計算方法などを知りたい人はhttps://円周率.jp/ を見るといいんじゃないんでしょうか。(この記事を書く上で大いに参考にさせていただきました。ありがとうございます。)

ちなみに書いた後に気づいたんですがhttps://trap.jp/post/1961/ とめちゃめちゃネタかぶりしてました。涙。

明日の記事は@imoimo ,@mutv625です。楽しみ～