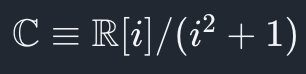この記事は新歓ブログリレー2025 37日目の記事です。
はじめに
皆さんごきげんよう。24Bのotimaです。数学の授業で複素解析は美しいといった先生が†定義†した複素数が天下り的な定義だったので逆張りで複素数体を実数体の多項式環の剰余環として†定義†しようと思います。
天下り的な定義
まず天下り的な定義を述べます。
実数の組 を と書く。この実数の組に対して、加法と乗法を
と定義する。これらの演算が定義された実数の組のことを複素数という。
これが定義です。確かにこの定義も対称性がどうとか思わないでもないですが、そもそも2乗すると となる数 を導入しようとしてこの定義は逆算的に考えないと出てこないと思います。そこで、実数体の多項式環の剰余環としての定義の方が自然で美しいと主張したいと思います。
美しい定義
実数体の多項式環 の極大イデアル による剰余体 を複素数体といい、その元を複素数という。
イデアル は素イデアル、多項式環 はユークリッド環なので単項イデアル整域であり、素イデアル は極大イデアルとなります。よって剰余環 は体であることがわかりますが、その辺りは†演習問題†としようと思います。
厳密なお話は参考文献に譲るととして、まず環というのは加法と乗法が定義されていてそれらの演算に分配法則などの整合性がある集合のことで、さらに 以外で割ることができる集合が体です。実数全体の集合は体です。環に係数を持つ多項式全体も環をなし、それを多項式環といいます。多項式環 は実係数多項式全体の集合という訳です。これで が導入されましたが、この を となるようにしたいです。そこで剰余環という概念が出てきます。環のイデアルという概念があり、環のイデアル による剰余環というのは、イデアル に含まれる元をと同一視するという集合のことです。例えば集合 は に の元をかけてできる元全体の集合を表し、これはイデアルです。このイデアルによる剰余環を考えた時、 に何をかけた値も とみなすということは とみなすということに他なりません。よって、 という集合上では とみなされます。この定義では を直接指定して定義しており、これはとても自然な方法だと思います。
多くの場合複素数体と剰余環 は同型であるという風に扱われますが、これを複素数の定義として採用するのも自然な定義でいいんじゃないかと思います。
おわりに
イデアル による剰余環だけでなく剰余環 を考えることにより自動微分など他にも可換環に関連した面白い話はありますが、今回は以上です。ありがとうございました。
明日の投稿者は@Hueterさんです。
参考文献
『代数学2 環と体とガロア理論』(雪江明彦)