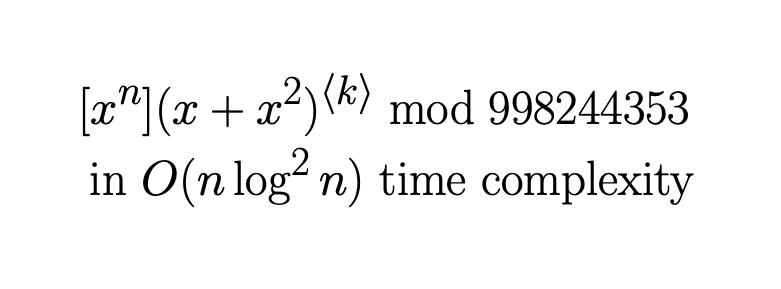はじめに

こんにちは。 22B の noya2 です。

私の誕生日である 6/28 に開催した yukicoder contest 435 の G 問題 で次のような出題をしました：

$[x^n](x+x^2{)}^{<k>}\mathrm{mod}998244353$ を求めよ（ ${\ast }^{<k>}$ は $\ast$ の $k$ 回合成 ）

以下、多項式や形式的冪級数（FPS）は $p=998244353$ として ${\mathbb{F}}_p$ 上で考えるものとします。

最近のことですが、 $n$ 次多項式 $f,g$ に対して、合成 $f\circ g$ の計算が $O(n{\log }^{2}n)$ 時間で計算できることが発明されました^[1]。このアルゴリズムと繰り返し二乗法をあわせれば、 $(x+x^2{)}^{<k>}\mathrm{mod}{x}^n$ を $O(n{\log }^{2}n\log k)$ 時間で計算できるということになります。本記事は $O(n{\log }^{2}n)$ 時間で計算する方法を提示します。また、中身が $x+x^2$ に限らない場合の拡張を示します。

$(x+x^2{)}^{<k>}\mathrm{mod}{x}^n$

重要になるのは次の等式です。ここで $\circ$ は関数の合成で、 $(f\circ g)(x)=f(g(x))$ です。

$$(x+x^2{)}^{<k>}\circ (x+x^2)=(x+x^2)\circ (x+x^2{)}^{<k>}(k=0,1,\dots )$$

両辺はいずれも $(x+x^2{)}^{<k+1>}$ に等しいです。このように合成冪は右合成と左合成を考えることによって非自明な式が得られることがあります。低次多項式の通常の冪 $f=g^k$ は、両辺を微分して非自明な式 $f^{\prime }g=kf{g}^{\prime }$ を得ていたことを思い出してください^[2]。これを $f$ の微分方程式とみなし、適切な初期条件をもとに $f$ の係数を低次から順に計算できたのでした。計算量が $k$ に依存しないという特徴もありました。これを踏まえて、同様に計算できないかを考えましょう。

$i=0,1,\dots$ について $[x^i]f$ を $f_i$ と書きます。 $f=(x+x^2{)}^{<k>}$ とおけば、上の式は

$$f(x+x^2)=f+f^2$$

$$⟺\sum _{i\ge 0}{f}_i(x+x^2{)}^i=\sum _{i\ge 0}{f}_i{x}^i+\sum _{i\ge 0}\sum _{j\ge 0}{f}_i{f}_j{x}^{i+j}$$

と書くことができます。両辺の $x^n$ の項の係数を比較すると

$$\sum _{0\le i\le n}{f}_i\left(\genfrac{}{}{0ex}{}{i}{n-i}\right)=f_n+\sum _{0\le i\le n}{f}_i{f}_{n-i}$$

となります。ここで $f_0=0,f_1=1,f_2=k$ に注意すると、 $f_n$ は相殺し、次のようになります。 $n\ge 4$ としておきます。

$$\sum _{i=0}^{n-2}{f}_i\left(\genfrac{}{}{0ex}{}{i}{n-i}\right)+(n-1)f_{n-1}=2f_{n-1}+\sum _{i=2}^{n-2}{f}_i{f}_{n-i}$$

よって、 $n-3<p$ のとき

$$f_{n-1}=\frac{1}{n-3}\left(\sum _{i=2}^{n-2}{f}_i{f}_{n-i}-\sum _{i=0}^{n-2}{f}_i\left(\genfrac{}{}{0ex}{}{i}{n-i}\right)\right)$$

に従って $f$ の係数を低次から順に計算できます。 $f_{n-1}$ が $f_0,f_1,\dots ,f_{n-2}$ から定まっていることに注意してください。

愚直な実装では $f\mathrm{mod}{x}^n$ の計算に $O(n^2)$ 時間かかることになりますが、もともと $f(x+x^2)=f+f^2$ の係数比較をしていたことを思い出しましょう。誤解を恐れず言えば、結局のところ $f(x+x^2),f^2$ の計算がオンラインでできればよいということになります。問題設定を明確にしましょう。

$x$ の多項式 $f$ が $f=0$ で初期化されている。 $q$ 個のクエリをオンラインで処理せよ。 $i(i=1,2,\dots )$ 回目のクエリでは $a_i\in {\mathbb{F}}_p$ が与えられる。 $f$ に $a_i{x}^i$ を加算し、 $[x^{i+2}]f(x+x^2),[x^{i+2}]f^2$ を求めよ。

$[x^i]$ ではなく $[x^{i+2}]$ を求めるという点で、通常の relaxed-convolution などとは設定が少し異なることに注意してください。先ほどの議論では、$[x^{[0,n-2]}]f$ から定まる $[x^n]f(x+x^2),[x^n](f+f^2)$ を比較して $[x^{n-1}]f$ を得ていたのでした。つまり、$2$ 項先の暫定的な結果を計算しておく必要があったのです。

これを踏まえて、次のような再帰関数 $D(l,r)$ を設計します。 $a=f(x+x^2),b=f+f^2$ とします。

• $[x^{[l,r-2]}]f$ を確定させる
• $[x^{[0,r-2]}]f$ から定まる $a,b$ の $[x^{[l,r-1]}]$ を計算する
• $\sum _{i=l}^{r-2}{f}_i(x+x^2{)}^{i-l}$ を返す

よくある分割統治FFTなどの実装と異なり、右端の項 $[x^{r-1}]$ を求めない定義になっています。

$D(l,r)$ の動作は次のとおりです。

1. $r-l\le 1$ のときなにもせず、 $0$ を返す。
2. $m=\lfloor (l+r)/2\rfloor$ とし、 $lhs=D(l,m)$ とする。
3. $[x^{[l,m-2]}]a$ から $[x^{[m,r-1]}]a$ への寄与と $[x^{[l,m-2]}]b$ から $[x^{[m,r-1]}]b$ への寄与を計算する。
4. $[x^{m-1}]f=\frac{1}{m-3}([x^m]a-[x^m]b)$ として $f_{m-1}$ を求める。
5. $[x^{m-1}]a$ から $[x^{[m,r-1]}]a$ への寄与と $[x^{m-1}]b$ から $[x^{[m,r-1]}]b$ への寄与を計算する。
6. $rhs=D(m,r)$ とする。 $lhs+rhs(x+x^2{)}^{m-l}$ を返す。

3.を終えた時点で $[x^{[0,m-2]}]a,[x^{[0,m-2]}]b$ から定まる $[x^m]a,[x^m]b$ が計算されていることに注目してください。また、4. で $m\le 3$ の場合は $f_0=0,f_1=1,f_2=k$ の結果を使います。

分割統治を行う際の統治部分では、 $[l,m)$ の寄与を $[m,r)$ へ送りますが、今回の場合は

• $[l,m-1)$ の寄与を先に送っておく
• その結果から $[m-1]$ を計算する
• $[m-1]$ の寄与を追加で送る

という挙動をすることになります。

$D(0,n+1)$ を呼べば $f\mathrm{mod}{x}^n$ が求められます。 $D(l,r)$ の統治処理は $O((r-l)\log (r-l))$ 時間で行えるので、あわせて $O(n{\log }^{2}n)$ 時間の計算量で求めることができます。

ここからは、いくつかの拡張（一般化）を見ていきます。

$(a+bx{)}^{<k>}\mathrm{mod}{x}^n$

アフィン変換の合成もまたアフィン変換です。行列累乗などで $O(\log k)$ 時間で計算できます。

$(a+bx+c{x}^2{)}^{<k>}\mathrm{mod}{x}^n(a\ne 0,c\ne 0)$

$2$ 次以上の非零項が存在し、さらに定数項が非零である場合、上述と同様の手法は通用しません。 $f=(a+bx+c{x}^2{)}^{<k>}$ とおいて $f(a+bx+c{x}^2)=a+bf+c{f}^2$ の $x^n$ の項の係数に注目すると、左辺は

$$[x^n]\sum _{i\ge 0}{f}_i(a+bx+c{x}^2{)}^i$$

ですが、これは $f_{n+1},f_{n+2},\dots$ に依存しています。

そもそも、定数項が非零である多項式やFPSをFPSの中に入れるような合成は、通常は定義できません（すべての項が収束しない）。オンライン合成の文脈でも、項が追加されるたびに、それまで計算した項がすべて更新されることになってしまいます。以下、定数項は $0$ であるとして進めます。

$(c{x}^2+O(x^3){)}^{<k>}\mathrm{mod}{x}^n$

$(c{x}^2+O(x^3){)}^{<k>}=c^{2^k-1}{x}^{2^k}+O(x^{2^k+1})$ となるため、　$k\in O(\log n)$ としてよく、素直な繰り返し二乗法で $O(n{\log }^{2}n\log \log n)$ 時間で計算できます。

$(bx+c{x}^2{)}^{<k>}\mathrm{mod}{x}^n(b\ne 0,b\ne 1,c\ne 0)$

例によって $f=(bx+c{x}^2{)}^{<k>}$ とおき、次の方程式を考えます。

$$f(bx+c{x}^2)=bf+c{f}^2$$

$$⟺\sum _{i\ge 0}{f}_i(bx+c{x}^2{)}^i=b\sum _{i\ge 0}{f}_i+c\sum _{i\ge 0}\sum _{j\ge 0}{f}_i{f}_j{x}^{i+j}$$

この式の $[x^n]$ を取ると

$$\sum _{i=0}^n{f}_i\left(\genfrac{}{}{0ex}{}{i}{n-i}\right)b^{2i-n}{c}^{n-i}=b{f}_n+c\sum _{i=0}^n{f}_i{f}_{n-i}$$

となります。 $f_0=0,f_1=b^k$ に注意すると $2\le n\le {\mathrm{ord}}_p(b)$ のとき

$$f_n=\frac{1}{b^n-b}\left(c\sum _{i=1}^{n-1}{f}_i{f}_{n-i}-\sum _{i=0}^{n-1}{f}_i\left(\genfrac{}{}{0ex}{}{i}{n-i}\right)b^{2i-n}{c}^{n-i}\right)$$

と定まります。両辺の $[x^n]$ から $[x^n]$ が定まっているため、より単純なオンライン畳み込み、中身が低次多項式のオンライン合成によって、 $O(n{\log }^{2}n)$ 時間で計算できます。 $b$ が入力で与えられる場合は $b$ の位数に注意が必要ですが、自然な文脈で出てくる場合は $b=-1,0,1$ 以外に注意するものはないかもしれません。

多項式が多少高次になる場合でも、 $1$ 次の係数 $b$ が位数の条件を満たせば、同様の手法で計算できます。

$(x+c{x}^2{)}^{<k>}\mathrm{mod}{x}^n(c\ne 0)$

$f_0=0,f_1=1,f_2=kc$ です。同様の考察によって、今度は $f_n$ は相殺しますが、$n\ge 4$ について

$$f_{n-1}=\frac{1}{(n-3)c}\left(c\sum _{i=2}^{n-2}{f}_i{f}_{n-i}-\sum _{i=0}^{n-2}{f}_i\left(\genfrac{}{}{0ex}{}{i}{n-i}\right)c^{n-i}\right)$$

を得ます。 $c=1$ のケースをはじめに扱っていたのでした。一般の $c$ でも実装はほとんど変わらないでしょう。計算量は変わらず $O(n{\log }^{2}n)$ 時間です。

多項式が多少高次になる場合でも、 $2$ 次の係数が非零である場合は、同様の手法で計算できます。

$(x+d{x}^3{)}^{<k>}\mathrm{mod}{x}^n(d\ne 0)$

そろそろ険しくなってきました。

$f_0=0,f_1=1,f_2=0,f_3=kd$ です。同様の考察によって、今度は $f_n,f_{n-1}$ は相殺しますが、 $n\ge 6$ について

$$f_{n-2}=\frac{1}{(n-5)d}\left(d[x^n]([x^{[0,n-3]}]f{)}^3-[x^n]([x^{[0,n-3]}]f)\circ (x+d{x}^3)\right)$$

を得ます。より複雑になりますが、 $3$ つ先の結果まで計算する分割統治によって実装できると思います。

多項式が多少高次になる場合で、しかも $1$ 次の係数が $1$ であって $2$ 次の係数が $0$ である場合でも、 $3$ 次の係数が非零であれば、なんとかなるというわけです。

$(-x+c{x}^2{)}^{<k>}\mathrm{mod}{x}^n(c\ne 0)$

例によって $f=(-x+c{x}^2{)}^{<k>}$ とおきますが、上と同様の方法では位数の条件から上手くいきません。そこで $2$ 回合成との右合成および左合成を考えましょう。つまり

$$f\circ (-x+c{x}^2)\circ (-x+c{x}^2)=(-x+c{x}^2)\circ (-x+c{x}^2)\circ f$$

$$⟺f\circ (x+2c^2{x}^3+c^3{x}^4)=(x+2c^2{x}^3+c^3{x}^4)\circ f$$

です。すぐ上に挙げたケース(高次になる場合)に帰着しました。

なお、一般に、 $1$ 次の係数を $b$ としたとき、 $(bx+c{x}^2{)}^{<{\mathrm{ord}}_p(b)>}=x+O(x^3)$ となって $2$ 次の係数は $0$ になるため、 $(x+c{x}^2{)}^{<k>}\mathrm{mod}{x}^n(c\ne 0)$ のケースに帰着させることはできません。

$(bx+O(x^2){)}^{<k>}\mathrm{mod}{x}^n,n>{\mathrm{ord}}_p(b)$

一般に、常にではないが漸化式の分母が $0$ になるケースです。この場合に対処する方法はわかりませんでした。また、実装が複雑になるくらいなら、そもそも $\log m$ 倍程度の時間をかけて素朴に合成と繰り返し二乗法を使った方が高速なのではないか、とすら思います。情報お待ちしております。

おわり

場合分けが大変になってしまいました。しかも結局のところ $(bx+c{x}^2{)}^{<k>}\mathrm{mod}{x}^n$ すら部分的にしか解けませんでした。残したケースは $c\ne 0,n>{\mathrm{ord}}_p(b)$ のケースです。

部分問題として登場した、少し先の項を求めるオンライン畳み込み・低次多項式のオンライン合成は、目新しくて気に入っています。

実は、想定解の実装は、出題時に tester をしてくださった potato167 さんに全てを担当していただきました。本当にありがとうございます。