undo可能uf でも値変更・値集約がしたい!

競技プログラミング界隈においてundo可能uf/dsuと呼ばれるデータ構造があります。本記事では、undo可能dsuに追加で頂点の値集約・かつ値の1点変更を実現する事を目標として、dsuの形を2分木に制限するデータ構造を提案します。そして、計算量は悪化するものの、実際にlibrary checkerのDynamic Graph Vertex Add Component Sumがそれなりに高速に解けている事を見ます。

この記事で説明するデータ構造について

以下の関数を備えたデータ構造を設計する事を目指します。
要素数 $n$ の頂点集合に対し
merge(u, v) ... 頂点 $u, v$ がそれぞれ属する連結成分を合成し、一つの連結成分とする。計算量 $O (lo g^{2} n)$
same(u, v) ... 頂点 $u, v$ が同じ連結成分に属しているかを返す。計算量 $O (lo g^{2} n)$
leader(u) ... 頂点 $u$ が属する連結成分の代表を返す。計算量 $O (lo g^{2} n)$
undo(u, v) ... 直前のmergeを呼ぶ直前の状態にデータ構造を戻す。但し、後述のsetによる頂点の値変更は戻さない。計算量 $O (lo g^{2} n)$
get(u) ... 頂点 $u$ が属する連結成分の頂点の値全てを、ユーザーが定義する演算opにより集約した値を返す。計算量 $O (lo g^{2} n)$
set(u, val)...頂点 $u$ の値をvalに変更する。 $O (lo g^{2} n)$

undo可能dsuとは

dsuのunion by rank/sizeのみを実行し、経路圧縮をしない物を指しています。
関数名は次です。
merge(u, v) ... 頂点 $u, v$ に、 $u, v$ が非連結ならば辺を張る。また、たとえ辺が張られなかったとしても、呼ばれたmergeは1回のmergeとして後述のundoの対象とする。
leader(u) ... 頂点 $u$ が属する連結成分の代表を返す。また、この頂点は内部で管理されているグラフの根に対応する。
undo() ... 直前のmergeを呼ぶ直前の状態にデータ構造を戻す。

値集約・値変更とは + 記号の定義

値集約 : 連結成分について、全ての頂点の値に対し何らかの演算を適応した値です。
値変更 : 頂点と値を指定して、その頂点の値を指定した値に変更する事を指しています。
本記事では簡単のため、次の2つのタイプを引き合いに出します。

type1 : 演算...+ 変更...代入

要は、連結成分内の頂点の値の合計値です。

type2 : 演算...max 変更...代入

要は、連結成分内の頂点の値のmaxです。

また、以後は $n$ 頂点のグラフに対するこのようなクエリを考えることとし、ufと言ったらundo可能dsuを指すことにします。さらに、本記事では木の高さは0から始まるとします。例えば1頂点の木の高さは0で、2頂点の木の高さは1です。

前置き: 普通のundo可能dsuではダメなのか

実は、type1のクエリについて、普通のufでも高速に処理することが出来ます。
まず、ufに追加で次の値を保持してもらいます。
a[v] := 頂点 $v$ の値
acc[v] := ufが管理する木において、頂点 $v$ の部分木の値の集約結果
次に、値の変更を(1)今の連結成分に反映 (2)undoが来た際、分裂した2つに正しく反映の2段階に分けて考えます。
まず(1)について、これは愚直にやってしまって良いです。なぜなら、undo可能dsuが内部に持つ木について、高さが $O (lo g n)$ で抑えられることから、連結成分の代表、つまり根まで遡ったとしても計算量が抑えられる為です。よって、根まで遡りながらaccの値を変更していくことで $O (lo g n)$ で実現可能です。
次に(2)について、これは+演算の持つ逆元から実現が可能です。詳しくは、頂点 $u, v$ の辺を切るとした時、acc[u] -= acc[v]とすれば良いです( $u$ が $v$ の親です。)。

ここで、type2についても同様の事を実行しようとすると、maxに逆元が無いことにより(1), (2)の段階が実行できない事に気づくと思います。
他の手段として値を集約し直すという手が考えられますが、通常のufではグラフの子の数に制約が無いため、一度のundoに $O (n)$ かかるケースが作成可能だと思います。

なお、本筋からは外れますが、type2において、値の変更がないならば普通のundo可能dsuで実現可能な事も観察できると思います。

本題: 形を2分木に制限する

type2のクエリを捌けるようにするために、ufのもつグラフの形を2分木に制限する事を考えます。
通常のufでは、merge(u, v)をleader(u)とleader(v)の間に辺を貼ることで処理しました。ここで、次のルールを導入しましょう。なお、以後特に断りがない場合、union by sizeによって親と子を分けた後に、 $u$ が親で $v$ が子とします。

merge(u, v)改 : leader(u)とleader(v)の間に辺を貼る。但しleader(u)が既に $2$ つの子を持っている場合、leader(u)から見て一番高い所にある、子の数が2未満の頂点のうち任意の頂点とleader(v)の間に辺を貼る。

これによって2分木の形が守られることは自明です。かつ、"上の方から埋めていく"という制約から、ある程度の頂点の密度は担保されていそうな感じがします。実際、手を動かしてみると、少ない頂点集合に対しては中々の充填率という気がします。(今気が付きましたが、例の中にいくつか偽物が混じっています。最初はunion by sizeではなく他の評価関数を用いていたのですが、途中からunion by sizeでも通ると気づいて変更した弊害です。ごめんなさい。)

非常にシンプルなアイデアだと思います。本記事では、このアイデアを元にufを改造します。

実装:実装を詰めます。

普通のufと比べて余分に必要になるのは次の操作です。
[1]部分木の頂点であって、子を2つ持たない頂点のうち、一番高いところにある頂点の取得
[2]木を上に登りながらの値の更新

これを実現するために、次の情報を持ちます。
par, lch, rch ... 親、左の子、右の子。この情報を元に、木を実際に動きながら値を更新します。
sz ...木の頂点数。この情報を元にmergeする際の親・子を決めます。
lv ...自分の部分木を見た際、完全二分木となっている部分の高さ　を持ちます。これは子を2つ持たない頂点のうち、一番高いところにある頂点の取得の用途に用います。
acc, A ... 冒頭の通りです。ufで管理する木における部分木の頂点全ての値を集約した値と、自分の値です。
his ... undoのための情報を持ちます。

merge/undoに伴うこれらの情報の修正が精々 $O (∣ 木の高さ ∣)$ で済みます。愚直に木を上に登りながら更新すれば良いです。
また、基本的な関数の設計は、後に実装を含んだリンクを提示することで説明とさせていただきます。
以下、補足です。
update(v) ... 頂点vから根に登りながら、各頂点の値を計算し直す関数です。ufの連結成分それぞれの根が持つ値が正しい、という状況が崩れた時に即座に呼びます。
merge(u, v)... 頂点leader(u), leader(v)に辺を貼ります。この際、whileの中で木を降りながら「1番上にある、まだ子を持てる頂点」を探しています。

また以下に、私が自己満足の為に実施した定数倍改善のお話を書きます。
まず、木を下るフェーズは再帰関数ではなくwhile文で十分です。
また、sz(=部分木のサイズ)について、これはupdate関数内で更新せずとも、根の値だけ正しく変更するような処理をすることができます。この処理の為に、update(v)の返り値で「vが属する連結成分の根」を返すようにしています。
及び、hisに持たせる情報について、これは辺を張った2頂点の番号のみで十分undoが処理できます。

実測: Dynamic Graph Vertex Add Component Sum　に投げてみる

ところで世の中には、「考えるな、まず計測せよ」という、「考えるな、感じろ」みたいなノリの言葉があった気がします。なので、計算量を考える前に一度問題を解いてみます。時間を見るついでに、このアルゴリズムに穴がある可能性を減らせたら嬉しいです。

というわけで、投げてみます。
https://judge.yosupo.jp/submission/212999
結果は395msです。説明をします。
まず本提出では、offlineのdynamic connectivityをしています。
よって、計算量は $O ((l ink の回数 + c u t の回数) \times lo g (クエリ 3 の回数) \times (u f の 1 回の m er g e ・ u n d o にかかる計算量))$ となります。伝わっておりますでしょうか？
これだけを見ても良くわかりませんね。
参考までに、通常のundo可能dsuを用いた実装での提出、及びoffline_connectivityのbuildまでやってufでの処理をしない提出、入出力だけする提出をそれぞれ提示します。
https://judge.yosupo.jp/submission/212940
https://judge.yosupo.jp/submission/213004
https://judge.yosupo.jp/submission/213006
通常のufの提出も説明をすると、この提出の計算量は $O ((l ink の回数 + c u t の回数) \times lo g (クエリ 3 の回数) \times lo g n)$ です。
これらについて、link_and_cutのケースについて纏めた物が以下の表になります。

種類	全体の実行時間	ufの処理時間
入出力だけ	53ms	0ms
uf以外の処理	115ms	0ms
通常のuf	157ms	42ms
改造uf	395ms	280ms

このケースでは大体7倍程遅くなっている事が見て取れます。

これらの計測結果から、ufの1回のmerge・unfoにかかる計算量(つまり、木の高さ)は、定数の重いlogかlog^2で抑えられそうだという予想が立ちます。また、ACが頂けたことから、ひとまず頓珍漢なことは言ってなさそうだなと安心が出来ます。ただ、このジャッジにこの解法に対するコーナーケースが入っている事を期待するのは少し無理がある気もするので、有利環境下に限った話では？という疑念は残りますが...。

本題2: 計算量解析

ではこれからは、計算量の話をします。結論から述べると、 $n$ 頂点の改造ufの木の高さは $lo g_{2}^{2} n$ で抑えられ、尚且つ $Θ (lo g^{2} n)$ の高さを与えるような操作列が存在します。

木の高さが $lo g^{2} n$ で抑えられること

mergeする前の木の高さが $lo g_{2}^{2} (木のサイズ = 頂点数)$ で抑えられるならば、mergeした後の木も $lo g_{2}^{2} (新たな木のサイズ)$ で抑えられる事を示します。

それぞれサイズが $a, b$ の二つの木 $A, B$ をmergeする事を考えます。一般性を損なわずに $a \geq b$ とします。ここで、 $A, B$ それぞれの高さを $h_{a}, h_{b}$ と置いた時

h_{a} \leq lo g_{2}^{2} a

h_{b} \leq lo g_{2}^{2} b

が成立していると仮定します。

ここで、union by sizeの原則よりAの下にBをつける事になるのですが、この時,「Aに含まれる頂点であって、子を2つ持たない頂点のうち一番上に有るもの」の高さは上から $⌊ l o g_{2} a ⌋$ で抑えられます(注意: 高さは0から始めています。)。このことは、「Aに含まれる頂点であって、子を2つ持たない頂点のうち一番上に有るもの」より高さが上の部分に関して、完全ニ分木でなければならないことからわかります。或いは、完全二分木に頂点番号を振っていくことで感覚的に理解できます。
よって、mergeして出来た木の高さは、mergeの時に辺の分1高さが増えることも加味して

ma x (lo g_{2}^{2} a, lo g_{2} a + 1 + lo g_{2}^{2} b)

で抑えられます。maxの左側は、AがBに対してはるかに巨大な場合かつ隙間がある場合などです。
あとは、これが $lo g_{2}^{2} (a + b)$ で抑えられることを言えば完了です。今、 $a, b$ は $1$ 以上の整数ですから、maxの左の場合は自明です。maxの右の場合について

f (a) = lo g_{2}^{2} (a + b) - (lo g_{2} a + 1 + lo g_{2}^{2} b)

が0以上である事を示す事を目標に、f(a)を $a$ について微分してみましょう。すると、

f^{'} (a) = \frac{2 lo g _{2} ( a + b )}{( a + b ) ln ( 2 )} - \frac{1}{a ln ( 2 )}

= \frac{2 a lo g _{2} ( a + b ) - ( a + b )}{a ( a + b ) ln ( 2 )}

が現れます。まず、f'(a)が常に非負である事を示します。
この関数の分子g(a)をもう一度aについて微分します。つまり、

g (a) = 2 a lo g_{2} (a + b) - (a + b)

f^{'} (a) = \frac{g ( a )}{a ( a + b ) ln ( 2 )}

に対し

g^{'} (a) = 2 lo g_{2} (a + b) + \frac{2 a}{( a + b ) ln ( 2 )} - 1

が現れます。今、 $a \geq b$ より、 $ln (2) \leq 0.7$ から g'(a)は

g^{'} (a) \geq \frac{2 a}{( a + b ) ln ( 2 )} - 1 \geq \frac{2 a}{a + a} - 1 \geq 1 - 1 \geq 0

から常に非負です。よって、

g (a) \geq g (b) = 2 b lo g_{2} (2 b) - 2 b

= 2 b (lo g_{2} (2 b) - 1) \geq 2 b (1 - 1) \geq 0

からg(a)は $a \geq b$ で常に非負となり、以上から

f^{'} (a) = \frac{g ( a )}{a ( a + b ) ln ( 2 )} \geq 0

が従います。
$a \geq b$ より、 $a = b$ の時がf(a)の最小値です。尚且つ、この値をみると

f (a) \geq f (b) = lo g_{2}^{2} 2 b - (lo g_{2} b + 1 + lo g_{2}^{2} b)

= (1 + lo g_{2} b)^{2} - (lo g_{2} b + 1 + lo g_{2}^{2} b)

= lo g_{2} b \geq 0

です。
および、一つも辺がない最初の状態において、高さが0から始まっている事に注意すると、木の高さが $lo g_{2}^{2} (木のサイズ)$ で抑えられています。
以上より、木の高さが $lo g_{2}^{2} n$ で抑えられることが示されました。

$Θ (lo g^{2} n)$ の高さを与えるような操作列が存在する事

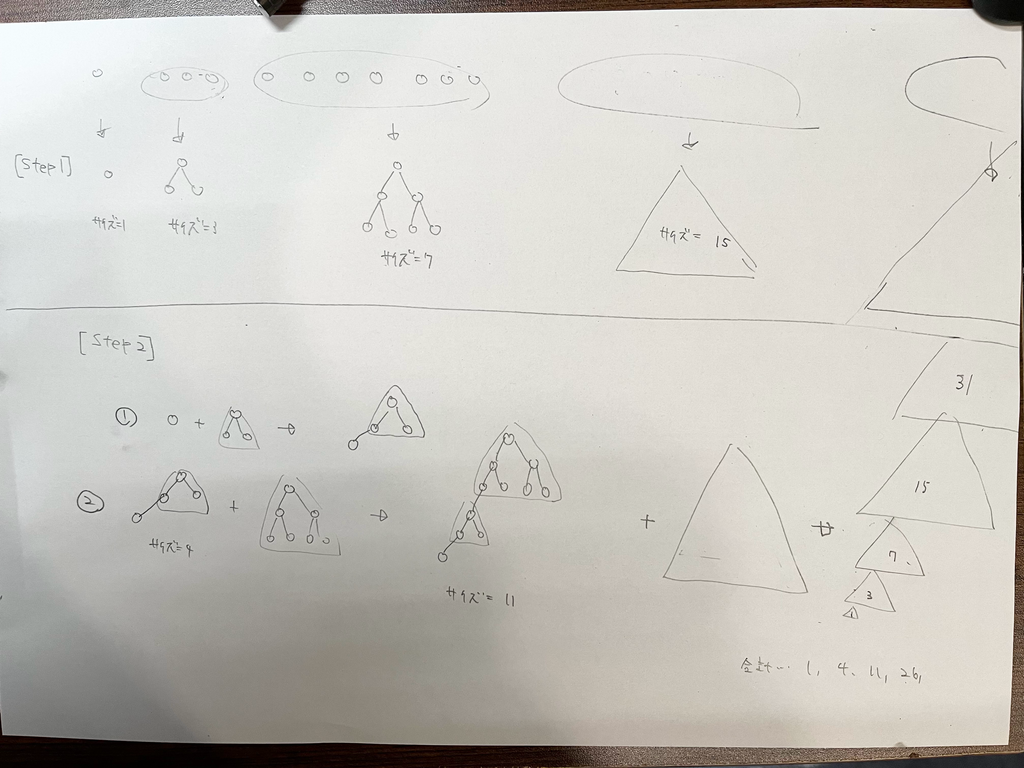
構築の時間です。結論から述べますと、次の図です。

木のサイズが2冪 - 1 となっていて、 $n$ の2進数での桁数と同じぐらいの段重なっていることがわかりますでしょうか。また、それぞれの段の高さは $0, 1, 2, 3,,,, (l o g n に近い値)$ となりますから、この木の高さは(mergeの際に辺の分高さが増える事も忘れずに計算して)

(0 + 1) + (1 + 1) + (2 + 1) + .... + ((l o g n に近い値))

となって $Θ (lo g^{2} n)$ です。

あとがき

この改造ufに対するコーナーケースが $n$ 回程度のmergeで作れてしまうことが判明してしまいました。この子が日の目を浴びることはあるのでしょうか。
其れはともかくとして、この改造ufは敵意を持っていない相手に対して、そのオーダーに比べ実行時間制限に間に合う程度には高速に動作する可能性が高いと言えるでしょう。実用上高速、というやつでしょうか？
この改造ufが実用に挙がる日は来るのでしょうか？
其れはそうと、あまり敵対視せずに仲良くして下さると幸いです。
参考までに、この改造ufを用いた提出をいくつか提示します。　　対策されていない可能性が高いという前提の元、まあまあ速いです。
通常uf(228ms) https://atcoder.jp/contests/abc356/submissions/54140282
改造uf(436ms) https://atcoder.jp/contests/abc356/submissions/54237026

通常uf(421ms) https://codeforces.com/gym/100551/submission/264143200
改造uf(546ms) https://codeforces.com/gym/100551/submission/264164017

この記事の内容につきまして何かお気づきになった点や気になった点がございましたら、もし宜しければ下部のコメント欄よりご連絡頂けると幸いです。
おまけ : 式変形の正当性について、chatgpt先生にお伺いを立てて見た所、概ね正しいのではないかというご意見をいただきました。ありがとうございます。https://chatgpt.com/share/89f11f32-f69b-4a88-8784-8319325816ce
なんか、私が真心込めて書き上げた式よりも生成された式の方が見易くないですか？誠に遺憾です。

参考文献

offline dynamic connectivity https://ei1333.github.io/luzhiled/snippets/other/offline-dynamic-connectivity.html

編集記録

2024/06/05 6時頃
「merge(u, v)改 : leader(u)とleader(v)の間に辺を貼る。但し、 $u$ が既に $2$ つの子を持っている場合、 $u$ から見て一番高い所にある、子の数が2未満の頂点のうち任意の頂点と $v$ の間に辺を貼る。」を「merge(u, v)改 : leader(u)とleader(v)の間に辺を貼る。但しleader(u)が既に $2$ つの子を持っている場合、leader(u)から見て一番高い所にある、子の数が2未満の頂点のうち任意の頂点とleader(v)の間に辺を貼る。」に修正

2024/06/05 9時頃
タイトルをundo可能dsuからundo可能ufに変更

2024/06/05 11時頃
undoの説明を変更。頂点の連結性を戻すのであって、値の変更は戻さない

2024/06/13 19時頃
数式の見た目を整えた

追記

2024/06/05 7時頃
せっかくなので、union by rankも試してみました。https://judge.yosupo.jp/submission/213045 (451ms)
よくわかりませんが、劇的に速くなる・遅くなることは無さそうだと思いました。

2024/06/07 8時頃
折角なので、内部の木を平衡2分木で管理するバージョンを作ってみました。木の高さが $O (lo g n)$ なので、殆どの操作が $O (lo g n)$ です。
参考資料 : https://www.slideshare.net/slideshow/2-12188757/12188757
提出例 : https://judge.yosupo.jp/submission/213404
はいこれだけではよくわかりません。
というわけで、手元で最悪ケースを作って実験してみました。
https://www.dropbox.com/scl/fi/z8dz6kps1qzuxrsn7wqar/test.txt?rlkey=ftpdn4fex1wxepf6w6ko8qrus&st=ajo7hrdr&dl=0
最悪ケースを作ったのち、頂点0にひたすら値クエリを飛ばしています。n = 262125, q = 362124です。
そして、この結果が
改造uf : 2.8秒
平衡uf : 2.8秒
と殆ど区別かつかない物でした。
原因の考察として、木の高さに
改造uf : 152
平衡uf : 42前後
と3, 4倍程度の開きしかないことから、他の定数倍で打ち消しあっているのだと思います。
試しに n = 524268としても差がつかない状況は変化しませんでしたので、どちらを使っても大差ないと思います。
なお、だからと言って改造ufが速いわけでもなく、上記の通り n, qが3 * 10 ^ 5付近であっても2秒を越えさせられたので、出来れば使わないというのが最善の策かと思いました(かなしい)

2024/06/09 2時頃
実は、06/05に記載したコードのrankを計算する部分がバグっていました。すみません。
それはさておき、いきなりですが、評価関数をunion by rankから union by 「新しくできる木の高さ」に変更してみます。どうなるでしょうか。
https://judge.yosupo.jp/submission/213714
中々速いです。そして、本文中で述べた最悪ケースに関して、こちらのコードは木の高さを23で抑えることに成功しました。
よって、こちらの評価関数を用いた場合、有意に高速化がなされるかもしれません。

2024/07/09 2時頃
改造ufの木の高さについて、どのような選択関数(どちらを親にするかを決める関数)を用いたとしても、高さが $Θ (lo g^{2} n)$ になるケースが作れると思います。通常のunion-findの時と同様、1頂点から初めて、同じものをマージしてできたものをまたマージして...というのを繰り返してみて下さい。