おしながき

• はじめに
• RerootingDP
• 設計の意図
• おわり
• 謝辞

はじめに

辺や頂点の重みを考慮して全方位木DPを抽象化するひとつの方法を紹介します。全方位木DPの説明はしません。
AtCoder Library のドキュメントに準い、要件と使用法を述べます。

RerootingDP

木に対して全方位木DPを行います。次の問題を解きます。

頂点 $0,1,\dots ,n-1$ からなる $n$ 頂点の木 $T$ が与えられます。
有向グラフ $G=(\mathbb{V},\mathbb{E})$ は以下を満たします。

• $\mathbb{V}=\{0,1,\dots ,n-1\}$ である。
• $\mathbb{E}\subset \mathbb{V}\times \mathbb{V}$ である。辺 $(a,b)$ は頂点 $a$ から頂点 $b$ への有向辺。$T$ において頂点 $a,b$ の間に辺が張られているとき, またそのときに限り $(a,b),(b,a)\in \mathbb{E}$ である。

また、各有向辺には整数値の番号が割り当てられていて、$\mathrm{idx}:\mathbb{E}\to \mathbb{Z}$ によって定められます。ここで ${\mathbb{E}}_{\mathrm{idx}}=\{\mathrm{idx}(e)|e\in \mathbb{E}\}$ としておきます。

可換モノイド $(E,\oplus :E\times E\to E,e\in E)$ と集合 $V$ および $put\_edge:V\times {\mathbb{E}}_{\mathrm{idx}}\to E,put\_vertex:E\times \mathbb{V}\to V$ が与えられます。次の擬似コードに従って計算される値 dfs(0,0), dfs(1,1),...,dfs(n-1,n-1) を求めてください。ただし、頂点 $r$ を根と見たときの頂点 $v$ の子の頂点の集合を $\mathrm{child}(r,v)$ とします。

V dfs(vertex r, vertex v){
   E prod = e();
   for ( (v, c) in E, c in child(r,v) ){
       prod = merge(prod, put_edge(dfs(r,c),idx(v,c)));
   }
   return put_vertex(prod, v);
}

この問題を時間計算量 $\mathrm{O}(n)$ で解くことができます。

また、このライブラリはオラクルとして merge, e, put_edge, put_vertex を使用しますが、これらが定数時間で動くものと仮定したときの計算量を記述します。オラクル内部の計算量が $\mathrm{O}(f(n))$ である場合はすべての計算量が $\mathrm{O}(f(n))$ 倍となります。

コンストラクタ

RerootingDP<E, V, merge, e, put_edge, put_vertex> g(int n);

• 可換モノイドの型 E
• DPの値の型 V
• $\oplus :E\times E\to E$ を計算する関数 E merge(E a, E b)
• $e$ を返す関数 E e()
• 辺番号 $i$ の辺を付加する関数 E put_edge(V x, int i)
• 頂点番号 $v$ の頂点を付加する関数 V put_vertex(E x, int v)

を定義する必要があります。

• 頂点数 n の木を作る準備をします。n 頂点 $0$ 辺のグラフを作ります。
• デフォルトでは n = 0 です。

制約

• $0\le n\le 10^8$

計算量

• $\mathrm{O}(n)$

add_edge

void g.add_edge(int u, int v, int idx, int xdi)

• 頂点 u から頂点 v への辺番号が idx である辺を追加します。
• 頂点 v から頂点 u への辺番号が xdi である辺を追加します。

制約

• $0\le u,v<n$
• ちょうど $n-1$ 回 add_edge を呼んでできるグラフは連結（どの $2$ 頂点間にもパスが存在する）であり、その後 add_edge は呼ばれない。

計算量

• ならし $\mathrm{O}(1)$

build

V g.build(int v)

• 上述した問題における dfs(v,v) を返します。

制約

• build を呼ぶ前にちょうど $n-1$ 回 add_edge を呼んでいる。
• build は $1$ 回までしか呼ばれない。

計算量

• $\mathrm{O}(n)$

reroot

vector<V> g.reroot()

• 長さ $n$ の配列 answers を返します。answers[v] は上述した問題における dfs(v,v) です。

制約

• reroot を呼ぶ前にちょうど $1$ 回 bulid を呼んでいる。
• reroot は $1$ 回までしか呼ばれない。

計算量

• $\mathrm{O}(n)$

使用例

AC code of https://atcoder.jp/contests/dp/tasks/dp_v

submission https://atcoder.jp/contests/dp/submissions/46008749

#include<bits/stdc++.h>
#include<atcoder/modint>
using namespace std;
using mint = atcoder::modint;


template <class E, class V, E (*merge)(E, E), E (*e)(), E (*put_edge)(V, int), V (*put_vertex)(E, int)>
struct RerootingDP {
    struct edge {
        int to, idx, xdi;
    };
    RerootingDP(int n_ = 0) : n(n_), inner_edge_id(0) {
        es.resize(2*n-2);
        start.resize(2*n-2);
        if (n == 1) es_build();
    }
    void add_edge(int u, int v, int idx, int xdi){
        start[inner_edge_id] = u;
        es[inner_edge_id] = {v,idx,xdi};
        inner_edge_id++;
        start[inner_edge_id] = v;
        es[inner_edge_id] = {u,xdi,idx};
        inner_edge_id++;
        if (inner_edge_id == 2*n-2){
            es_build();
        }
    }
    vector<V> build(int root_ = 0){
        root = root_;
        vector<V> subdp(n); subdp[0] = put_vertex(e(),0);
        outs.resize(n);
        vector<int> geta(n+1,0);
        for (int i = 0; i < n; i++) geta[i+1] = start[i+1] - start[i] - 1;
        geta[root+1]++;
        for (int i = 0; i < n; i++) geta[i+1] += geta[i];
        auto dfs = [&](auto sfs, int v, int f) -> void {
            E val = e();
            for (int i = start[v]; i < start[v+1]; i++){
                if (es[i].to == f){
                    swap(es[start[v+1]-1],es[i]);
                }
                if (es[i].to == f) continue;
                sfs(sfs,es[i].to,v);
                E nval = put_edge(subdp[es[i].to],es[i].idx);
                outs[geta[v]++] = nval;
                val = merge(val,nval);
            }
            subdp[v] = put_vertex(val, v);
        };
        dfs(dfs,root,-1);
        return subdp;
    }
    vector<V> reroot(){
        vector<E> reverse_edge(n);
        reverse_edge[root] = e();
        vector<V> answers(n);
        auto dfs = [&](auto sfs, int v) -> void {
            int le = outs_start(v);
            int ri = outs_start(v+1);
            int siz = ri - le;
            vector<E> rui(siz+1);
            rui[siz] = e();
            for (int i = siz-1; i >= 0; i--){
                rui[i] = merge(outs[le+i],rui[i+1]);
            }
            answers[v] = put_vertex(merge(rui[0],reverse_edge[v]),v);
            E lui = e();
            for (int i = 0; i < siz; i++){
                V rdp = put_vertex(merge(merge(lui,rui[i+1]),reverse_edge[v]),v);
                reverse_edge[es[start[v]+i].to] = put_edge(rdp,es[start[v]+i].xdi);
                lui = merge(lui,outs[le+i]);
                sfs(sfs,es[start[v]+i].to);
            }
        };
        dfs(dfs,root);
        return answers;
    }
    private:
    int n, root, inner_edge_id;
    vector<E> outs;
    vector<edge> es;
    vector<int> start;
    int outs_start(int v){
        int res = start[v] - v;
        if (root < v) res++;
        return res;
    }
    void es_build(){
        vector<edge> nes(2*n-2);
        vector<int> nstart(n+2,0);
        for (int i = 0; i < 2*n-2; i++) nstart[start[i]+2]++;
        for (int i = 0; i < n; i++) nstart[i+1] += nstart[i];
        for (int i = 0; i < 2*n-2; i++) nes[nstart[start[i]+1]++] = es[i];
        swap(es,nes);
        swap(start,nstart);
    }
};

mint merge(mint a, mint b){
    return a * b;
}
mint e(){
    return mint(1);
}
mint put_edge(mint v, int i){
    return v + 1;
}
mint put_vertex(mint e, int v){
    return e;
}

int main(){
    int n, m; cin >> n >> m;
    mint::set_mod(m);
    RerootingDP<mint,mint,merge,e,put_edge,put_vertex> g(n);
    for (int i = 0; i < n-1; i++){
        int u, v; cin >> u >> v;
        g.add_edge(u-1,v-1,i,i);
    }
    g.build();
    for (auto ans : g.reroot()) cout << ans.val() << endl;
}

設計の意図

全方位木DPはすべての部分木 $t$ に対する答え $dp(t)$ を高速に求めるアルゴリズムで、$t$ に含まれるさらに小さい部分木 $s$ に対する答え $dp(s)$ から $dp(t)$ を計算していきます。$r$ を全体の根としたときの木DPの値を求める際、$v$ の部分木を有向辺 $(par(v),v)$ に対応させると理解しやすい、という話があります。（ $par(v)$ は $r$ を根としたときの $v$ の親です。 $v=r$ のときは $par(v)$ は仮想的な頂点であり、有向辺 $(par(v),v)$ は仮想的な辺です。 ）これに基づいて、有向辺 $(u,v)$ に対応する答えを $f(u,v)$ と書くことにしましょう。$u=-1$ のときは仮想的な有向辺を考えており、対応する部分木は $v$ を根とする根付き木です。さて、このライブラリの設計では、

$$f(u,v)=\underset{c\in \mathrm{child}(u,v)}{⨁}f(v,c)$$

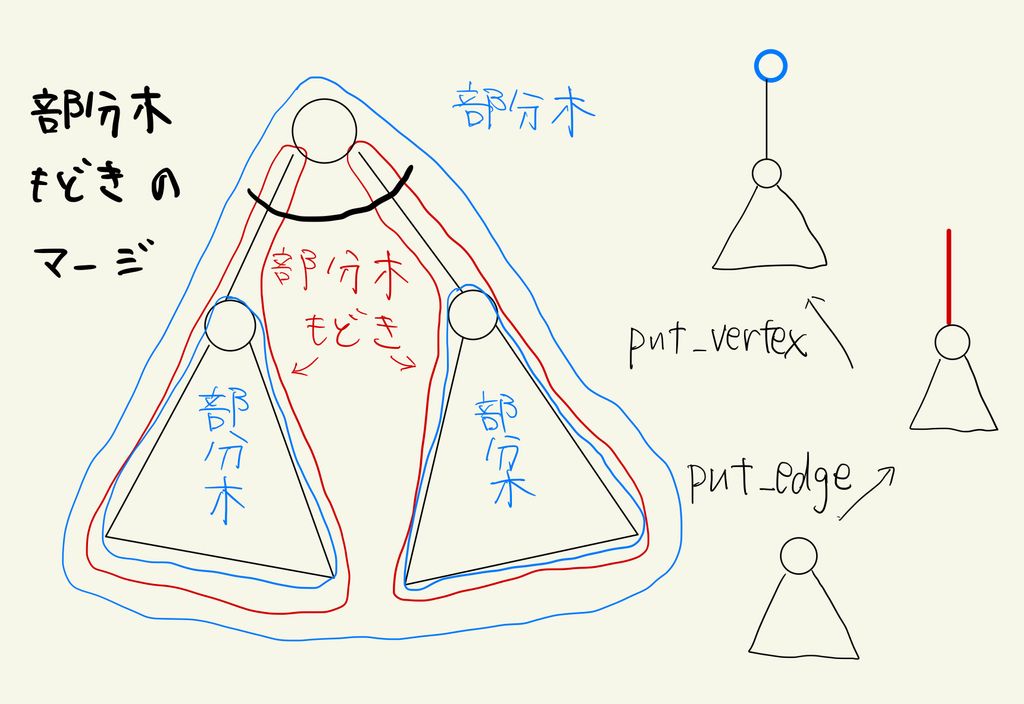
のような遷移式では考慮されない「辺の重み」を取り入れるため、補助的な関数 $g(u,v)$ を定義しています。$g(u,v)$ は $(u,v)$ に対応する部分木に辺 $(u,v)$ を付加するが頂点 $u$ はまだ付加しないみたいな（雰囲気で感じ取ってください）部分木もどきに対する答えっぽいもの（雰囲気で感じ取ってください）です。要点は次のとおりです。

• 部分木に辺を付加すると、部分木もどきになる。($put\_edge$)
• 部分木もどきをマージして頂点を付加すると、部分木になる。($put\_vertex$)
• $f(u,v)=put\_vertex\left(\underset{c\in \mathrm{child}(u,v)}{⨁}put\_edge(f(v,c),\mathrm{idx}(v,c)),v\right)$

ライブラリ内で辺に重み E e 、頂点に重み V v を持つような設計もあり得ると思ったのですが、できるだけライブラリの外側で問題依存パートを扱いたいのと、 put_vertex には単位元のようなものを要求しないため初期値の設定に困ったので、頂点・辺番号を引数に渡す関数を要求するライブラリの設計にしました。

実装上の工夫(追記 : 2023/09/28)

内部で保持する木の構造を二次元配列から一次元配列で持つように変更しました。
また、左右で累積を取る reroot 内部の処理を、右側の累積のみ記録するように変更しました。

おわり

抽象化の方法は唯一ではないです。より良い設計があれば教えてください。また、記事のわかりにくいところや誤りなどを発見されましたら、ご一報くださると大変ありがたいです。

謝辞

この記事のレビューをしてくれる方、ありがとうございます。先に感謝しておきます。