こんにちは、すく(0214sh7)です。
東工大数学系の4年生で、traPではアルゴリズム班のリーダーをやっています。そろそろ引退
東京工業大学プログラミングコンテスト2022 に運営・作問者として参加しました。そこに出題した問題にエルハート多項式を用いるものがあるのですが、エルハート多項式についてを簡潔にまとめてみたくなったのでこの記事を書いています。
ところで、ピックの定理はご存知ですか?
ピックの定理
ピックの定理
平面上の凸多角形 は、その頂点の座標がすべて整数で、
- (位相的な)内部にある座標が整数である点の個数が
- (位相的な)境界にある座標が整数である点の個数が
であるとき、その面積 は
で表される。
この定理は発見者であるゲオルク・アレクサンダー・ピック(Georg Alexander Pick)の名前からピックの定理と呼ばれています。小学校で習うこともあります。
この定理は実は 次元以上の多次元に拡張することができます。それを説明するにあたり、まずは多角形の拡張を説明しましょう。
多面体
多面体の定義は主に二通りありますが、今回はそのうち頂点記述と呼ばれる方法を使います。
もう片方は超平面記述と呼ばれています。
次元空間 上の集合 が多面体(polytope) であるとは、 の有限個の点 の凸包として が表せることを言います。つまり、
で表せるような のことを多面体と呼び、 と書きます。また、 を の頂点(vertex)といいます。
多面体の他にも前提知識がいくつかあるので並べます。
格子点
ユークリッド空間 の部分集合 は格子(lattice,束とは異なる)と呼ばれる集合の代表例であり、今回は の元、つまり全ての座標が整数である点を格子点(lattice point)と呼ぶことにします。
拡大
の部分集合 について、その 次拡大( th dilation) とは、
で定義される集合のことです。
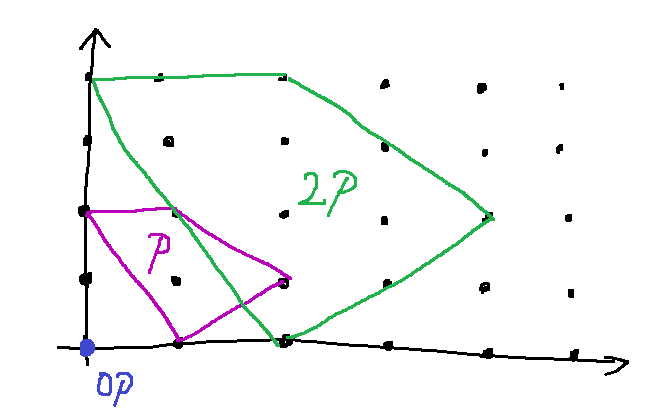
次拡大は原点のみから成ります。
凸
集合 が凸(convex)であるとは、任意の と実数 について が満たされることを言います。
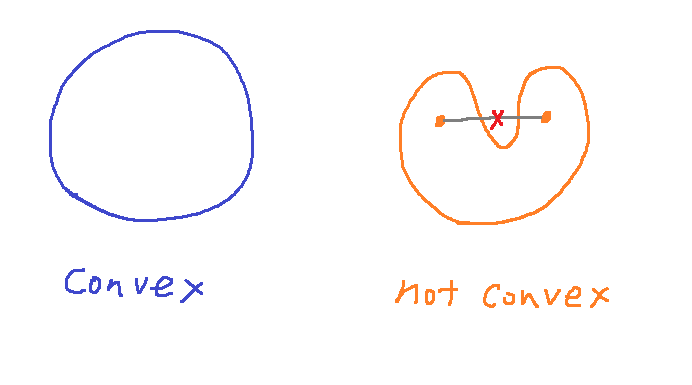
左は凸ですが、右は灰色の線分がはみ出すので凸ではありません。
整
多面体 が整(integral)とは、 の頂点がすべて整数座標、つまり格子点であることを言います。
離散体積
多面体 に含まれる格子点の個数を離散体積(dicrete volume)といいます。
そして、 次拡大 の離散体積を と書きます。( )
例1
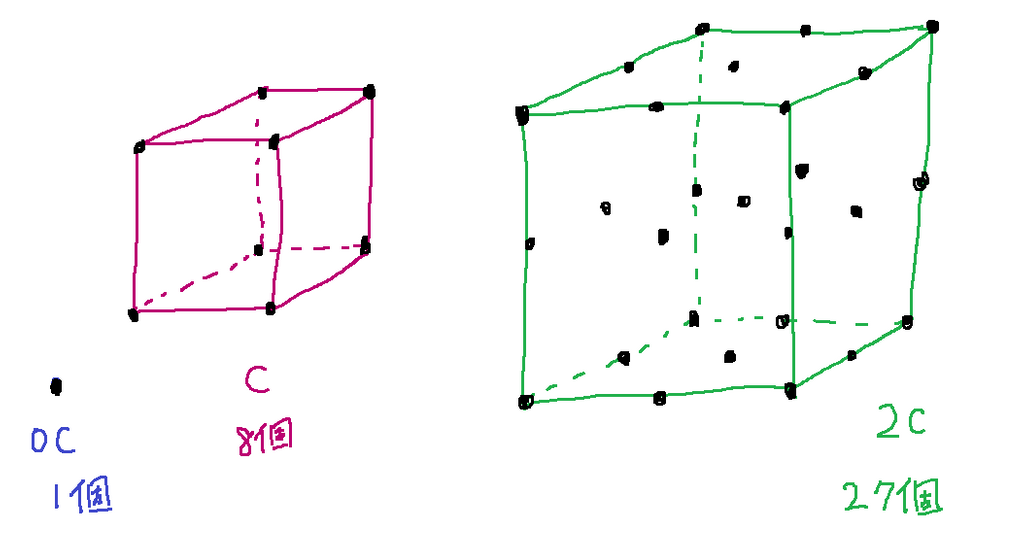
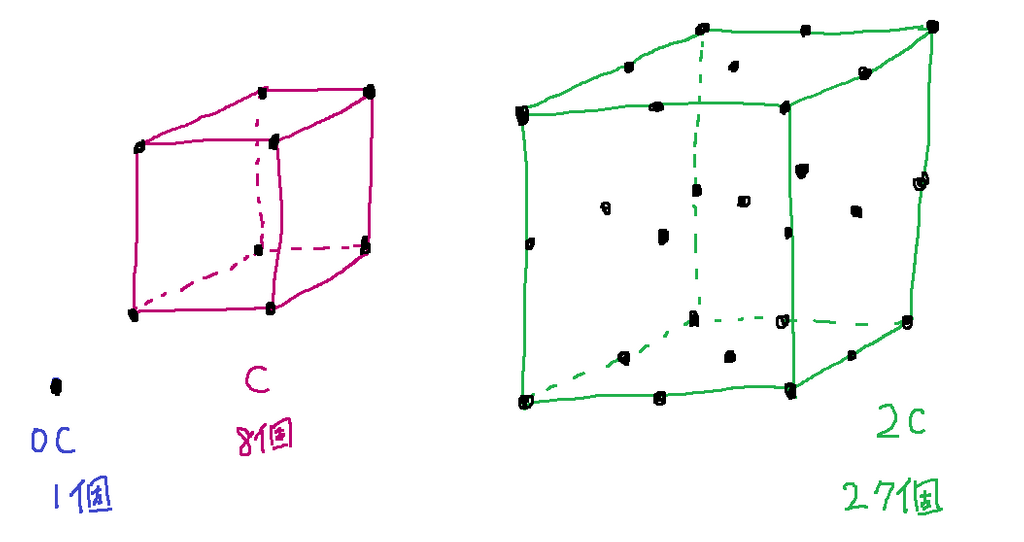
たとえば、立方体 を考えます。
には つの格子点 が含まれているため です。
同様に には格子点が 個含まれており です。同様に、 であることを調べることができます。
例2
四面体 を考えます。
には格子点が つ含まれており です。
には格子点が 個含まれており です。
には格子点が 個含まれており です。
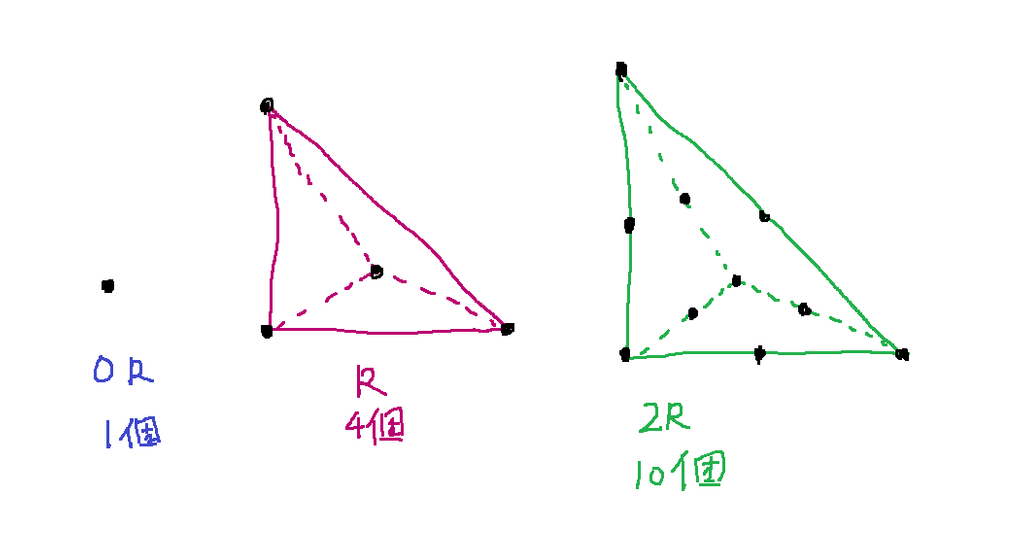
以上の つの例では がともに多項式になっています。実はこれらは多くの多面体において多項式になるのです!
エルハート多項式
エルハートの定理
次元整凸多面体 について、 は について 次多項式になる。
この定理はこれを証明したフランスの数学者ウジェーヌ・エルハート(Eugène Ehrhart)にちなんでエルハートの定理と、 はエルハート多項式(Ehrhart polynomial)と呼ばれています。
証明を書こうと思ったのですがとてもここで書けるようなボリュームじゃなかったので諦めました。
Springerの"Computing the Continuous Discretely"(
Matthias Beck, Sinai Robins)という本に書いてあるので興味がある方はそちらをご覧ください。
このため、 がわかっていれば多項式補完によってエルハート多項式を求めることができます。さらに定義から はすべて整数なので、多項式の係数はすべて有理数になります。
しかし、 次拡大 は原点のみから成るので、 であることはすぐにわかります。
実装する際には が小さかったり、どの を使うのかが決まっていることが多いので、ヴァンデルモンド行列の逆行列を埋め込むとよいでしょう。
他にも、エルハート多項式を求めるための便利な性質を紹介します。
先頭係数
次元整凸多面体 のエルハート多項式を とする。
このとき、先頭係数 は の体積と一致する。
これを証明するには、 を示すとよいでしょう。これはリーマン積分と同じノリで を小さなキューブで近似するとわかります。
多面体の頂点からうまく体積を求められればエルハート多項式を求めるために必要な情報が一つ減ります。
たとえば 次元多面体については表面を構成する三角形(ポリゴン)がわかれば体積が求まるので先頭係数を求めることができます。
例1
立方体 のエルハート多項式は であり、その先頭係数 は の体積と一致しています。
例2
四面体 のエルハート多項式は であり、その先頭係数 は の体積と一致しています。
エルハート-マクドナルドの相互法則
エルハート-マクドナルドの相互法則
次元凸整多面体 とその(位相的な)内部 、正整数 に対し、
が成り立つ。
これを エルハート-マクドナルドの相互法則 (Ehrhalt-Macdonald reciprocity) といいます。
このため、 またはその拡大 の内部の格子点の個数がわかっていれば のエルハート多項式の負の項を調べることができるわけですね。
例1
1辺の長さが の立方体 を考えます。
には格子点が 個含まれており、その内部には つだけあります。
また 次拡大 には格子点が 個含まれています。
このため、
がわかります。
多項式補完によって が求まります。
次拡大 には格子点が 個含まれており、これは と一致します。
例2
一般の多角形( 次元多面体) のエルハート多項式を考えてみましょう。
の内部の格子点の数を 、 の境界の格子点の数を とします。すると
なので、 として
なので、これを解いて
になります。なので、 です。
先述したように先頭係数 は の面積 なので、
と書くこともできます。特に、
が成り立っており、これはピックの定理そのものです。
おまけ
次元多面体に対して、
- 内部の格子点の数
- 境界の格子点の数
- 体積
からエルハート多項式を求めることができます。考えてみましょう!
おわりに
ちなみに多面体 が凸かつ頂点が有理数座標なら、 は準多項式(quasipolynomial)になり、やや面倒です。
本格的な作問はCPCTF22に続きTTPC2022が2回目なのですが、作問って楽しいですね。これを使う問題の作問の想定解書くのは苦行だったけどな!!!
いい数学ライフを!!!!!(半ギレ)