traPAdventCalendar2016の21日目担当のぱるまです。
この記事ではスプラトゥーンにおける確定数推移の基礎事項について紹介していきます。「確定数推移とは...?」と思う人も多いかもしれませんが、とりあえずスプラトゥーンに出てくるギアパワーの中の、攻撃と防御のギアパワーに関する話だという認識で大丈夫です。具体的には、
- 防御32で、敵の攻撃が何積みまでならスプシュー3発を耐えられるか?
- 攻撃25スプシューを使うと、敵の防御が何積みまでであればスプシュー3発で倒せるか?
といったような問題を解く方法を3種類紹介していきます。1つ目が「確定数推移のグラフ」を使う方法、2つ目が「確定数推移の表」を使う方法、3つ目が「100/ダメージ倍率の表」を使う方法です。1つ目と2つ目についてはスプラトゥーン(Splatoon) for 2ch Wiki*に載っているので知っている人がいるかもしれません。確定数推移のグラフや表、100/ダメージ倍率の表の作り方、使い方(問題の解き方)がこの記事のメインとなります。
途中、理論的な話が続くので、それより具体的な解き方を知りたいという人は適宜読み飛ばしてください。
スプラトゥーンのバージョンは、投稿時の最新であるVer2.12.0を仮定します。
目次
- 言葉の定義
- ダメージ倍率式
- ダメージ倍率境界
- 境界上の攻撃数、防御数
- 確定数推移のグラフ
- 確定数推移の表
- 100/ダメージ倍率の表
- 攻撃パターン
- 確定数推移のグラフ・表(フルバージョン)
- その他の事柄
- いろいろな問題
- 練習問題
- 参考にしたサイト
1. 言葉の定義
本題に入る前にまずは言葉の定義をします。
57表記
ある種類のギアパワーをどれだけ付けているかを表すときに、
[メインの数]×10 + [サブの数]×3
の値を使って表すことがあります。この表し方を57表記と言います。メイン1つの効果を10としたとき、サブ1つの効果は3に相当するので、57表記の値が大きければ大きいほどギアパワーの効果が大きくなります。
例えば、
メイン2、サブ4を57表記で表すと10×2 + 3×4 = 32となり、
メイン3、サブ9を57表記で表すと10×3 + 3×9 = 57となります。
最大量(メイン3、サブ9)積むと57になるため、57表記と呼ばれます。
冒頭で述べた、「防御32で、...」の防御32は57表記で表しています。今後、ギアパワーの数を表記する際には57表記を使用します。
メインの数は0から3、サブの数は0から9なので、57表記の値は次の40種類です。
0, 3, 6, 9, 10, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 41, 42, 44, 45, 47, 48, 51, 54, 57
攻撃数/防御数
57表記で表された攻撃のギアパワーの数を攻撃数、57表記で表された防御のギアパワーの数を防御数と呼ぶことにします。
基本ダメージ
攻撃や防御のギアパワーをつけていないときの1発のダメージを基本ダメージと呼びます。例えば、攻撃や防御のギアパワーをつけていないときのスプラシューターのダメージは35なので、基本ダメージは35となります。多くのブキで、発射してから敵に当たるまでの時間が長いとダメージが減衰しますが、この記事では減衰する前のダメージを考えることにします。
クイボのダメージ
クイボには、直撃、近距離爆風、遠距離爆風の3種類のダメージがあり、基本ダメージはそれぞれ、60、35、25となっています。ここでは、クイボの直撃をクイボ60、近距離爆風をクイボ35、遠距離爆風をクイボ25と基本ダメージ量を使って区別することにします。また、クイボ60とクイボ35で2回ヒットした場合の攻撃をクイボ60+35のように表記します。
攻撃パターン
攻撃の組み合わせを攻撃パターンと呼ぶことにします。
<例>
- 52ガロン2発
- スクスロ直撃 + 渦
- クイボ60 + シャプマネオ
- クイボ60+35
合計基本ダメージ
ある攻撃パターンに対する基本ダメージの総和を合計基本ダメージと呼ぶことにします。
<例>
- 「52ガロン2発」の合計基本ダメージ → 104
- 「スクスロ直撃 + 渦」の合計基本ダメージ → 114
- 「クイボ60 + シャプマネオ」の合計基本ダメージ → 88
<参考>
- 52ガロンの基本ダメージ→52
- スクスロ直撃の基本ダメージ→76
- スクスロ渦の基本ダメージ→38
- シャプマネオの基本ダメージ→28
ダメージ倍率
ダメージ倍率とは
[基本ダメージ]×[ダメージ倍率]=[実際のダメージ]
となるような倍率のことです。
例えば、基本ダメージは35、ダメージ倍率が0.95のとき、実際のダメージは33.25となります。
ダメージ倍率は攻撃を与える側の攻撃数と攻撃を受ける側の防御数から決まります。
確定数
例としてスプシューで考えます。イカのHPは100、スプシューの基本ダメージは35なので3発当てたら倒せます。何発当てたら倒せるかというのを確定数といい、この場合確定数は3であるといいます。もし、攻撃をする側の攻撃数が0で攻撃を受ける側の防御数が10の場合、1発のダメージ33.232となり、3発で倒せなくなり4発で倒せるようになります。このように防御を積まれると確定数があがることがあります。
2. ダメージ倍率式
次に、攻撃を与える側の攻撃数、攻撃を受ける側の防御数からダメージ倍率がどのようになるのかについて説明します。 を57表記の値として を次のように定義します。 攻撃を与える側の攻撃数を 、攻撃を受ける側の防御数を としたとき、ダメージ倍率 は次のようになります。

図1. y=f(x)のグラフ
なお、 または のとき、厳密には式(1)は成り立ちませんが、57積みをする人がほとんどいないため、ここでは簡単のために無視して考えます。(厳密に考えたい場合は の値を として計算する必要があります。) の式を平方完成すると次のようになります。 よって、 は次のように表されます。
3. ダメージ倍率境界
では本題に入ります。まずは冒頭でも述べた次の問題を考えます。
「防御32で、敵の攻撃が何積みまでならスプシュー3発を耐えられるか?」
イカのHPが100、スプシュー3発の合計基本ダメージは105ダメージ(1発が35ダメージ)なので、敵の攻撃数を としたとき、 すなわち、 が3発耐えるための条件になります。あとはこの条件を満たす最大の を求めればいいことになります。( は に関する2次式なので、2次不等式 を解けばよいことになりますが、2次不等式を解くのは面倒なので他の方法を使います。)
「攻撃25スプシューを使うと、敵の防御が何積みまでであればスプシュー3発で倒せるか?」という問題についても同様に考えられます。
敵の防御数を としたとき、 すなわち、 が3発で倒すための条件になります。あとはこの条件を満たす最大の を求めればいいことになります。
どちらの問題でも出てくる は合計ダメージがちょうど100となるようなダメージ倍率と言えます。これらの問題ではダメージ倍率と の大小関係が問題となっていて、 が倒せるかどうかのダメージ倍率の境界になっているといえます。
4. 境界上の攻撃数、防御数
合計ダメージがちょうど100ダメージとなるようなダメージ倍率を とし、 とします。こうなる攻撃数 と防御数 について考えます。つまり、こうなるような と は倒せるかどうかの境界にある攻撃数、防御数であるといえます。この境界より攻撃数が大きければ倒せる、防御数が大きければ倒せないとなります。ということで を満たすときの と の関係について見ていきます。
まずは のときを考えます。このとき、 を満たします。
よって、式(2)より つまり
グラフに表すと図2のようになります。(グラフは の例)
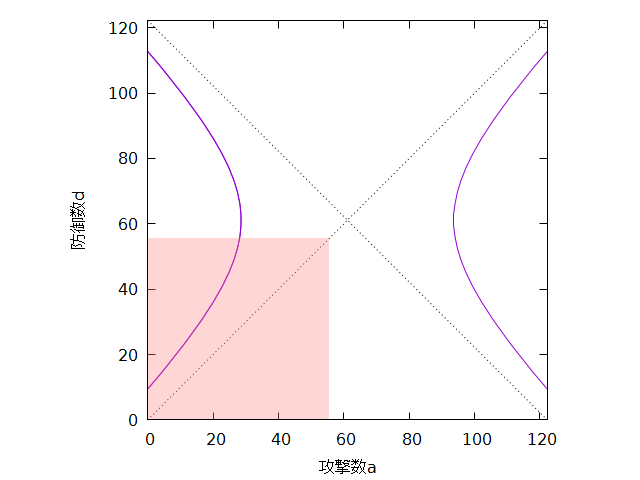
図2. 式(3)のグラフ なので、実際に考えるべきなのはグラフの赤い領域になります。
同様に考えると、 のときには次のようになります。
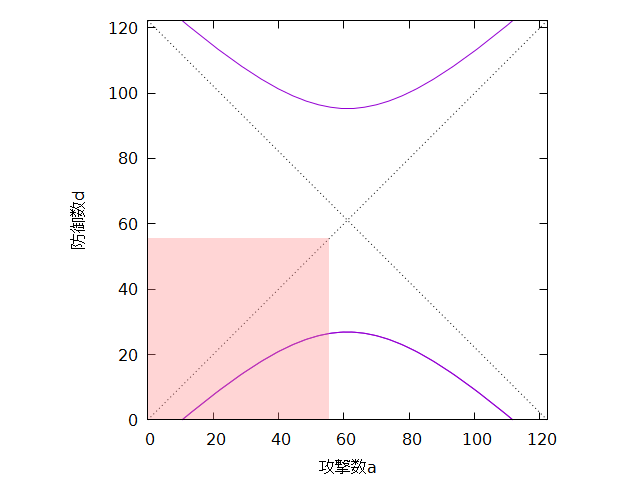
図3. 式(4)のグラフ
ちなみに、これらのグラフは双曲線になっていて、破線のような漸近線を持ちます。
次に範囲をちゃんと に制限して考えてみます。
式(3)、式(4)を に気をつけて について解くと次のようになります。
5. 確定数推移のグラフ
1つ目の例: スプシュー3発
式(5)をグラフで表してみます。スプシュー3発(合計基本ダメージ:105)で100ダメージとなるようなダメージ倍率 を考えると、式(5)のグラフは次のようになります。

図4. m=100/105の確定数推移のグラフ
このようなグラフは確定数推移のグラフと呼ばれています。このグラフは図2のグラフの一部なので、このグラフは双曲線の一部になっています。
このグラフ上にある点 がちょうど100ダメージとなる攻撃数 と防御数 になります。つまり、このグラフより上側にあるような ではスプシュー3発で倒せない、このグラフより下側にあるような ではスプシュー3発で倒せることになります。このグラフが倒せるかどうかの境界線となっています。(境界線上ではちょうど100ダメージになるので倒せます。)
例えば、攻撃を与える側の攻撃数が10、攻撃を受ける側の防御数30の場合、点 はグラフより上側にあるので、3発では倒せません。また、攻撃数が20、防御数が30の場合、点 はグラフより下側にあるので、3発で倒せます。
上側だと倒せるのか下側だと倒せるのかがわからなくなることがありますが、そういうときには、**防御数が多いほうが倒されにくくなる(または攻撃数が多いほうが倒しやすくなる)**ことを意識するとわかりやすくなると思います。
次に攻撃数を固定し、スプシュー3発で倒せるような防御数の範囲、スプシュー3発で倒せないような防御数の範囲について考えてみます。攻撃数を25で固定して考えると、次のようになります。
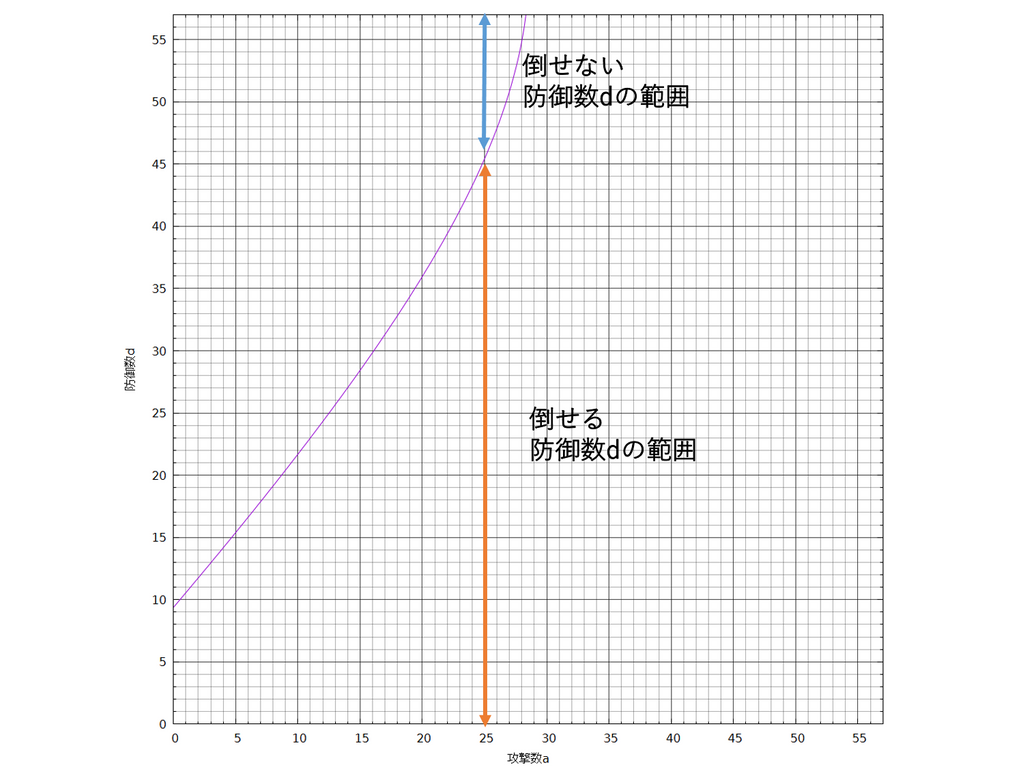
図5. 倒せる/倒せない防御数の範囲
この図から、防御数が0から45であればスプシュー3発で倒せ、防御数が46から57であれば倒せないというのがわかります。一般に、倒せる防御数の範囲は境界以下の範囲、倒せない防御数の範囲は境界より大きい範囲となります。倒せる防御数の範囲では倒せる防御数の範囲の最大値(xxまでにあたる値)、倒せない防御数の範囲では倒せない防御数の範囲の最小値(xxからにあたる値)が重要になります。今回の例で言うと、倒せる防御数の範囲の最大値は45、倒せない防御数の範囲の最小値は46になります。ただし、57表記で46となるようなメインとサブの組合せが存在しないため、倒せる防御数の範囲の最大値は47ということもできます。
「攻撃25スプシューを使うと、敵の防御が何積みまでであればスプシュー3発で倒せるか?」という問題は倒せる防御数の範囲(の最大値)を求める問題で、これにより45までであれば倒せるということがわかります。
また、「攻撃25スプシューを使うと、敵の防御が何積み以上であるとスプシュー3発で倒せないか?」という問題は倒せない防御数の範囲(の最小値)を求める問題で、これにより47以上であれば倒せないということがわかります。
次に攻撃39の場合で倒せる防御数の範囲、倒せない防御数の範囲を考えてみると、図3(または図4)のグラフより、すべての防御数(0から57)で倒せ、倒せない防御数は存在しません。
今度は逆に防御数を固定し倒せる防御数の範囲、倒せない防御数の範囲を考えてみます。防御数を32で固定して考えると、次のようになります。
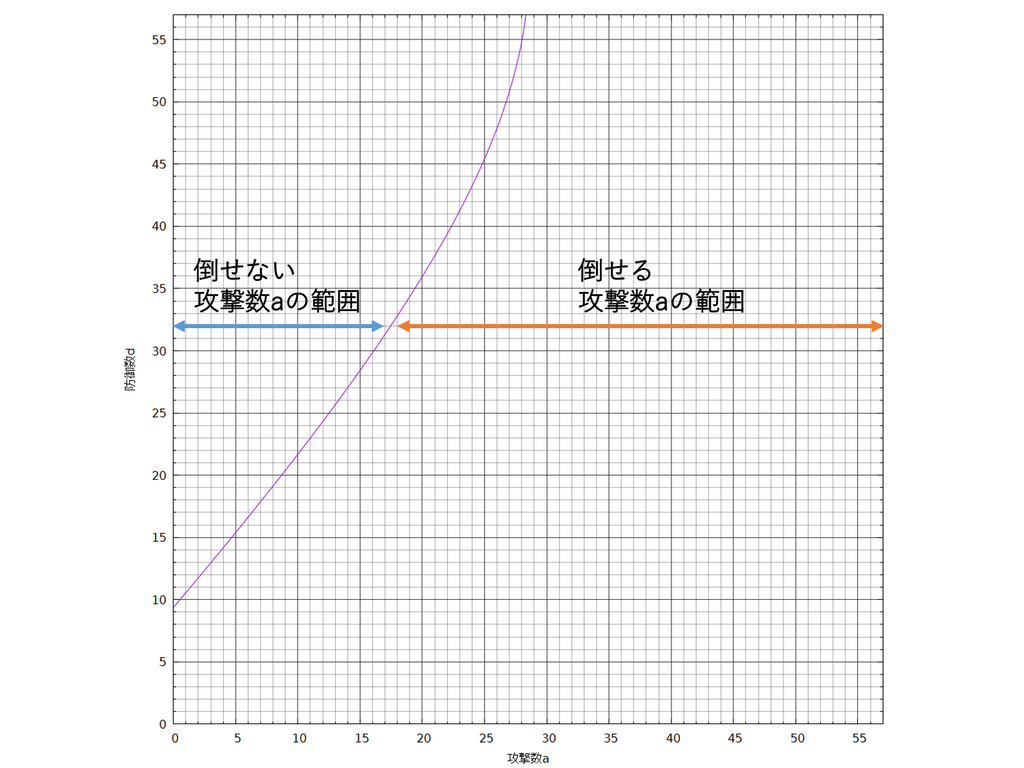
図6. 倒せる/倒せない攻撃数の範囲
この図から、攻撃数が0から17であれば倒せない、18から57であれば倒せるということがわかります。一般に、倒せない攻撃数の範囲は境界未満の範囲、倒せる攻撃数の範囲は境界以上の範囲となります。倒せない攻撃数の範囲では倒せない攻撃数の範囲の最大値(xxまでにあたる値)、倒せない防御数の範囲では倒せる攻撃数の範囲の最小値(xxからにあたる値)が重要になります。
「攻撃25スプシューを使うと、敵の防御が何積みまでであればスプシュー3発で倒せるか?」という問題に対しては防御17積みまでであればスプシュー3発で倒せると言えます。(なお、57表記で17となるようなメインとサブの組合せは存在しないため、実質防御16積みまでとなります。)
2つ目の例: クイボ60+35
今まではスプシュー3発を見てきましたが、次にクイボ60+35で見ていきます。合計基本ダメージは95になるので、100ダメージになるようなダメージ倍率 は となります。この場合、式(5)のグラフは次のようになります。
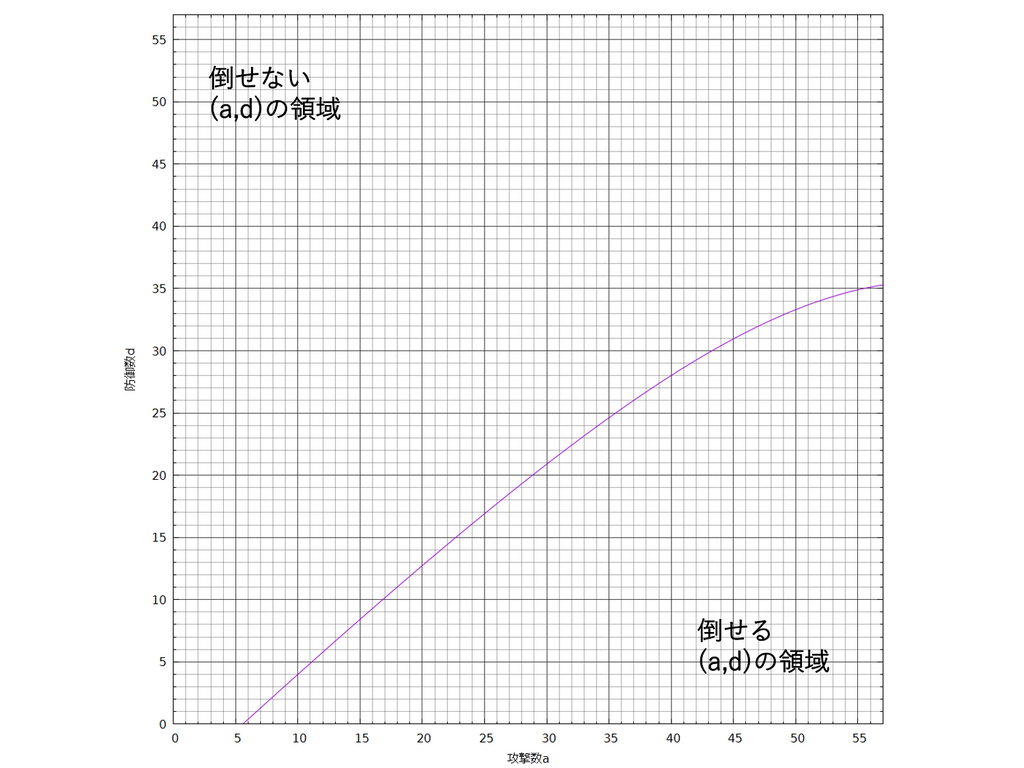 図7. m=100/95の確定数推移のグラフ
図7. m=100/95の確定数推移のグラフ
スプシュー3発のときと同様の考え方で、「防御32で、敵の攻撃が何積みまでならクイボ60+35を耐えられるか?」といった問題をこのグラフから求めることができます。
図4のグラフと図7のグラフで大きく異なるのは100ダメージになるようなダメージ倍率 が1未満(図4)か1より大きいか(図7)によります。 が1未満であれば図4のように直線 より上側にある傾きがだんだん大きくなるようなグラフを得ます。また、1より大きければ図6のように直線 より下側にあり、傾きがだんだん小さくなるようなグラフを得ます。
ここで確定数推移のグラフから何が求まるのかをまとめておきます。
- ある攻撃数に対する、倒せる防御数の範囲(0からxxまで。境界より下側。)
- ある攻撃数に対する、倒せない防御数の範囲(xxから57まで。境界より上側。)
- ある防御数に対する、倒せない攻撃数の範囲(0からxxまで。境界より左側。)
- ある防御数に対する、倒せる攻撃数の範囲(xxから57まで。境界より右側。)
ややこしいですが、
- 倒せる場合には、攻撃数は足りていて、防御数は足りていない
- 倒せない場合には、防御数は足りていて攻撃数は足りない
ということを念頭に置くか、確定数推移のグラフ(特に図5、図6)をイメージすると理解しやすくなると思います。
確定数推移のグラフの問題点
次に「攻撃9積み52ガロンを使うと、敵の防御が何積みまでであれば52ガロン2発で倒せるか?」について考えます。52ガロン2発の合計基本ダメージは104なので、100ダメージになるようなダメージ倍率は100/104になります。このときの確定数推移のグラフは次のようになります。
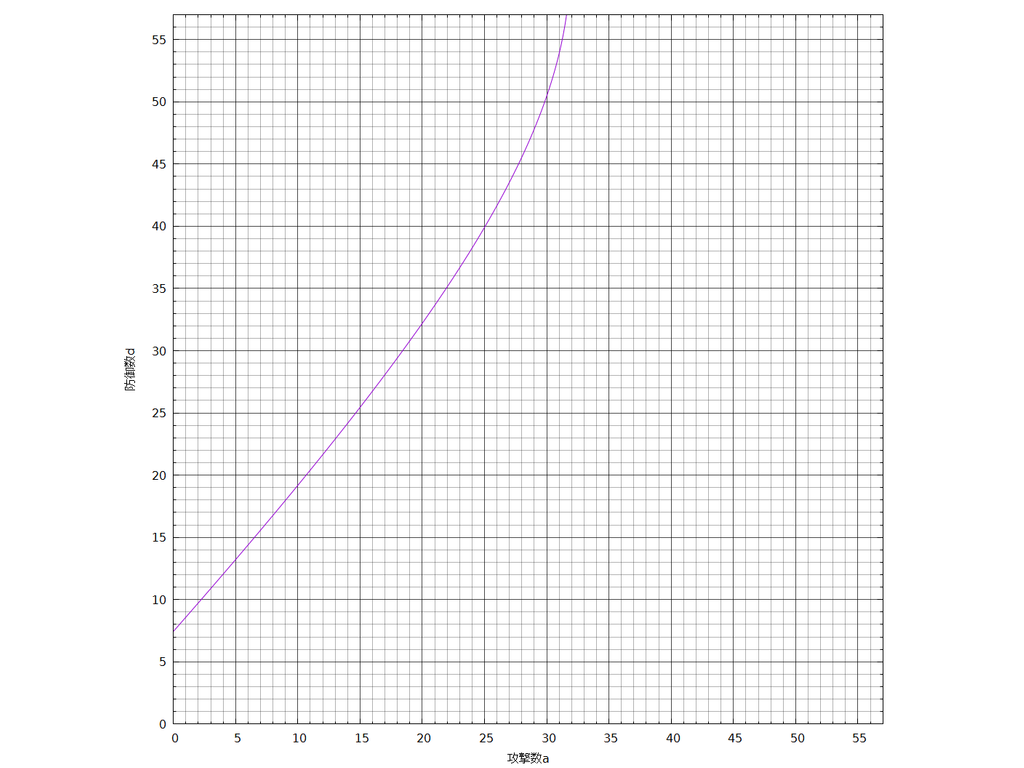 図8. m=100/104の確定数推移のグラフ
図8. m=100/104の確定数推移のグラフ
ここで1つ問題になるのは、点 はグラフより上側にあるのか、下側にあるのかです。グラフを見る限り、この点はグラフを通っているように見えます。つまり、防御18積みまでであれば2発で倒せるのか、防御16積みまでであれば2発で倒せるのかが表からだとわかりにくいです。(実際には、点 はグラフより上側にあるので、防御16積みまでが2発で倒せる防御数の範囲です。)
このようにグラフが格子点を通っているように見えて、どこまでが倒せる範囲でどこからが倒せない範囲なのかがわからないことがたまににあります。(たまになので、深刻な問題ではありません)
この問題を解決する手段としては次の3つの手段が考えられます。
- グラフの画像サイズをできるだけ大きく、グラフの線や格子線をできるだけ細く描画する。(見やすさとのトレードオフ)
- グラフを通っているように見える格子点があったら、その点がグラフより上側にあるのか下側にあるのかをグラフに明記する。
- 次に述べる確定数推移表を使用する。(確定数推移のグラフを数値化して表形式にしたもの)
なお、グラフが格子点を通っているように見えるような場合があっても、グラフが本当に格子点を通っていることは、 以外ではほとんどありません。ちなみに、 のときの確定数推移のグラフは直線 になります。
その他の攻撃パターンに対する確定数推移の表については9. 確定数推移のグラフ・表(フルバージョン)で提示します。
6. 確定数推移の表
先程のグラフを数値化して表形式にすることを考えます。
まずは「防御32で、敵の攻撃が何積みまでならスプシュー3発を耐えられるか?」という問題を考えます。このときには攻撃パターンがスプシュー3発、防御数が32のときの倒せない攻撃数の範囲の最大値を知りたいです。先程の確定数推移のグラフでも求めることができますが、攻撃パターン、防御数を入力として、倒せない攻撃数の範囲の最大値を出力とするような表をあらかじめ作っておくという方法もとれます。そのような表をどのように作るかを考えていきます。
まず、入力として与えられた攻撃パターンから、100ダメージになるようなダメージ倍率 が求まります。また、防御数 が入力として与えられています。つまり、 と から倒せない攻撃数の最大値を求めればよいことになります。求めるためには、確定数推移のグラフと同様に式(5)を使って倒せるかどうかの境界となる を求め、この より小さい最大の57表記を求めるという方法が1つあります。ただ、この方法だと次のような問題が発生します。
- が0から57の範囲にない場合の扱いが少し大変。( が虚数になる場合もある。)
- より小さい最大の57表記を求めるのが少し大変。
- 57表記57の場合でも正しくなるように厳密に考え、 を30として扱いたい場合に式(5)に場合分けを追加する必要があり大変。
- 誤差が怖い。
なので、この方法より計算時間はかかるが直接的である次の方法で求めます。
- 各57表記 (この記事の冒頭で列挙した40種類)に対して、ダメージ倍率 を式(1)から計算する。
- と を比較する。 のときには倒せて、 $r(a,d)
現実的には の値を大きい方(57)から順番に調べることになります。倒せるような が見つかればその値が求める最大値になります。
この方法を元にすると、攻撃パターンがスプシュー3発、防御数が0から57の57表記の値のときの倒せないような攻撃数の最大値の表は次のようになります。
表1. スプシュー3発で倒せないような攻撃数の最大値の表
| **防御数d** | **最大の 攻撃数a** |
| 0 | - |
| 3 | - |
| 6 | - |
| 9 | - |
| 10 | 0 |
| 12 | 0 |
| 13 | 3 |
| 15 | 3 |
| 16 | 3 |
| 18 | 6 |
| 19 | 6 |
| 20 | 6 |
| 21 | 9 |
| 22 | 10 |
| 23 | 10 |
| 24 | 10 |
| 25 | 12 |
| 26 | 13 |
| 27 | 13 |
| 28 | 13 |
| 29 | 15 |
| 30 | 16 |
| 31 | 16 |
| 32 | 16 |
| 33 | 18 |
| 34 | 18 |
| 35 | 19 |
| 36 | 20 |
| 37 | 20 |
| 38 | 21 |
| 39 | 21 |
| 41 | 22 |
| 42 | 23 |
| 44 | 24 |
| 45 | 24 |
| 47 | 25 |
| 48 | 26 |
| 51 | 27 |
| 54 | 27 |
| 57 | 28 |
表1から、「防御32で、敵の攻撃が何積みまでならスプシュー3発を耐えられるか?」に対する答えは、攻撃16積みまでなら3発耐えられるということになります。
他の攻撃パターンを追加する場合は、表1に列を追加すれば良いです。(追加したものはまとめて9. 確定数推移のグラフ・表(フルバージョン)で提示します。)
今考えたのが、「攻撃パターン、防御数に対する、倒せない攻撃数の範囲の最大値」でこれは「攻撃数がxxまでだと倒せない」のxxにあたる値です。
次の3つについても同様に表を作ることができます。
- 攻撃パターン、攻撃数に対する、倒せる防御数の範囲の最大値 (「防御数がxxまでだと倒せる」のxxにあたる値)
- 攻撃パターン、攻撃数に対する、倒せない防御数の範囲の最小値(「防御数がxx以上だと倒せない」のxxにあたる値)
- 攻撃パターン、防御数に対する、倒せる攻撃数の範囲の最小値(「攻撃数数がxx以上だと倒せる」のxxにあたる値)
これら4種類の表をまとめて確定数推移の表と呼ぶことにします。これらの具体的な表はまとめて9. 確定数推移のグラフ・表(フルバージョン)で提示します。
なお、この「確定数推移の表」と、次に出てくる「100/ダメージ倍率の表」を作る際には、厳密に考えても難しくならないため、 として計算することにします。
7. 100/ダメージ倍率の表
ある攻撃パターンに対して、ちょうど100ダメージになるようなダメージ倍率を とします。攻撃数を 、防御数を とすると、 のとき、その攻撃パターンで倒せてます。また、 のとき、その攻撃パターンでは倒せません。
条件式を書き換えると、 のとき、その攻撃パターンで倒せて、 のとき、その攻撃パターンでは倒せないことになります。 は通常、基本合計ダメージを表しています。例えば、スプシュー3発(合計基本ダメージは105)だと、 なので、 です。
よって、 の値と合計基本ダメージの大小関係で倒せるか倒せないかが分かります。言い換えると、 の値は、ある攻撃数、防御数の場合の倒すために必要な最低限の合計基本ダメージ(合計基本ダメージの境界値)であると言えます。
例えば、攻撃数が3、防御数が21の場合、 なので、基本合計ダメージが108.644未満であれば倒せない、108.644以上であれば倒せるということになります。
各攻撃数 、防御数 に対して、 を計算した表があると便利なのでその表を次に示します。
表2. 100/ダメージ倍率の表 (csvファイル)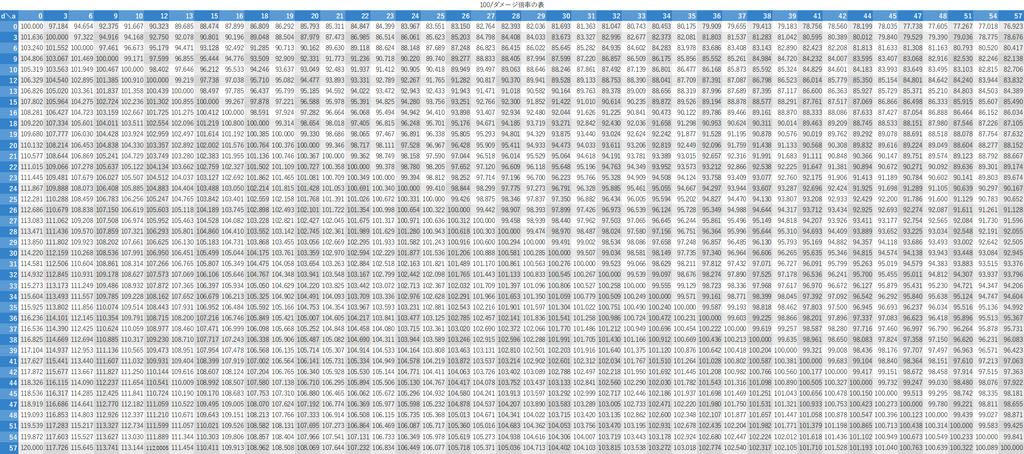
この表の値が、倒せるかどうかの合計基本ダメージの境界になっていて、この値以上の場合には倒せて、この値より小さい場合には倒せないということがわかります。例によって、「防御32で、敵の攻撃が何積みまでならスプシュー3発を耐えられるか?」という問題をこの表から求めてみます。まず、表の防御数(d)が32の行を見ます。横に見ていくと、攻撃数(a)が16のところの値が105.646、攻撃数が18のところの値が104.767になっています。スプシュー3発の合計基本ダメージは105なので、攻撃数が16までであればスプシュー3発で耐えられて、18以上であれば耐えられないことになります。
この例で求めたのは「防御数に対する、倒せる/倒せない防御数の範囲」ですが、同様に「攻撃数に対する、倒せる倒せない攻撃数の範囲」も求めることができます。 は一般に基本合計ダメージを表していると書きましたが、「クイボ60+銅モデ」などの場合ではメインのダメージ上限の影響で、 と基本合計ダメージが一致しません。( の求め方など詳しくは後述します)。この場合には基本合計ダメージではなく の値と表2の値を比較する必要があります。( の値を擬似的に合計基本ダメージとみなすと考えることもできます。)
確定数推移のグラフや確定数推移の表にはない100/ダメージ倍率の表のメリットとしては、この表が1つあれば、どのような攻撃パターンに対しても対応できることです。確定数推移のグラフの場合には、必要な攻撃パターンの数だけグラフを描画する必要があります。また、確定数推移の表の場合には必要な攻撃パターンの数だけ表の列が必要になります。
8. 攻撃パターン
どのような攻撃パターンを対象とするか
いままで攻撃パターンは、例としてスプシュー3発を中心に考えてきました。スプシュー3発以外で、どのような攻撃パターンについて確定数推移のグラフや表を求めていくかについて考えていきます。
攻撃をいくらつけても倒せない攻撃パターン、防御をいくらつけても倒される攻撃パターンについては考える必要がありません。つまり、考える攻撃パターンの対象は次の2つです。
- 通常倒されないが、攻撃をつけることによって倒せるようになりえる攻撃パターン。(例: クイボ60+35)
- 通常倒されるが、防御をつけることによって倒されなくなりえる攻撃パターン。(例: スプシュー3発)
ダメージ倍率の最大値は13/10(攻撃数57、防御数0)で、最小値は5/6(攻撃数0、防御数57)です。よって、合計基本ダメージが1000/13(≒76.92)以上であれば100ダメージ以上になりえて、120ダメージ未満であれば100ダメージ未満になりえます。よって、合計基本ダメージが76.92ダメージ以上、120ダメージ未満の攻撃パターンのみを考えればよいことになります。
ローラーやブラスターの爆風、チャージャーの途中撃ちのようにダメージが固定でなく、ダメージに多くの種類があるものについてはここでは考えません。ただし、クイボについては高々3種類のダメージ(60、35、25)しか無いため考えます。
クイボ60+シャプマネオのようにメインとサブの組合せの攻撃パターンについては考えますが、すべての場合を考えるとキリがないので、メインとクイボの組合せの一部のみをこの記事では取り扱います。
100ダメージになるようなダメージ倍率
確定数推移の表やグラフを作るためには、各攻撃パターンに対して、100ダメージとなるようなダメージ倍率 の値が必要です。これは、合計基本ダメージ に対して、 と計算すれば普通は求まります。普通でない場合とは、メインのダメージ上限を考慮しなければいけない場合です。
メインのダメージ上限
シューターなどのブキには、ダメージ上限が設けられています。例えば、モデラーの場合、基本ダメージは24.5ですが、攻撃積みで確定数が下がらないようにするために24.9がダメージ上限になっています。つまり攻撃パターンとしてモデラー4発を考えると、合計基本ダメージは98なので76.92以上120未満の範囲に入っていますが、攻撃をつけることによって倒せるようになるわけではないので、これは対象外となります。
メインとサブの組合せの攻撃パターンで、徐々にダメージ倍率を上げていくと、100ダメージに達する前にメインのダメージ上限に達する場合があります。この場合、100ダメージになるようなダメージ倍率 が、合計基本ダメージ に対して と計算できなくなります。
例として、「クイボ60+銅モデ」の攻撃パターンで考えます。合計基本ダメージは60+24.5=86.5です。メインがダメージ上限(24.9)に達するようなダメージ倍率は24.9/24.5≒1.016です。ダメージ倍率が1.016のとき、この攻撃パターンのダメージは86.5×1.016=87.884です。よって、この攻撃パターンでは、徐々にダメージ倍率を100ダメージに達する前にメインのダメージ上限に達します。ダメージ倍率が100ダメージになるようなダメージ倍率 のとき、メインはダメージ上限に達しているので、メインのダメージは24.9となります。よって、 なので、 となります。
「クイボ60+銅モデ」の例のように、徐々にダメージ倍率を上げていくと、100ダメージに達する前にメインのダメージ上限に達する場合、通常一致する合計基本ダメージと の値が一致しません。「クイボ60+銅モデ」の例で言うと、合計基本ダメージは86.5ですが、 です。よって、「7. 100/ダメージ倍率の表」でも書きましたが、表2の「100/ダメージ倍率の表」を使う際には注意が必要です。この場合、表2の値と比較すべきなのは合計基本ダメージではなく です。
今度は「クイボ60+L3D」の攻撃パターンを考えます。L3Dの基本ダメージは29で、ダメージ上限は33.3です。クイボ60+L3Dの合計基本ダメージは89です。よって、メインがダメージ上限に達するダメージ倍率は33.3/29 ≒ 1.148です。ダメージ倍率が1.148のとき、クイボ60+L3Dのダメージは89×1.148=102.172です。よって、この攻撃パターンでは100ダメージに達したときにはまだメインのダメージ上限に達していません。つまり、100ダメージになるようなダメージ倍率 は100/89(=1.12360)です。
メインとサブの組合せの攻撃パターンについては、このようにして100ダメージに達する前にメインのダメージ上限に達する可能性を考慮する必要があります。サブをクイボ1発に限れば、100ダメージに達する前にメインのダメージ上限に達してしまい、100ダメージになるようなダメージ倍率 が合計基本ダメージ に対して と計算できないのは、次の2つの攻撃パターンがあります。( の値は次に提示する表3に掲載)
- クイボ60+銅モデ
- クイボ60+ジェッカス
(ただし、メインにダメージ上限がある影響で100ダメージに達しない攻撃パターンは他に存在して、例えば「クイボ25+シャプマネオ2発」や「クイボ35+銅モデ2発」などがあります。)
他のパターン(例として上げた「クイボ60+L3D」など)に関しては、 で計算できます。
対象とする攻撃パターンの一覧
以上をふまえ、この記事では次の表3に列挙する攻撃パターンについて扱います。(ついでに合計基本ダメージなども載せておきます。)
表3. この記事で扱う攻撃パターンの一覧など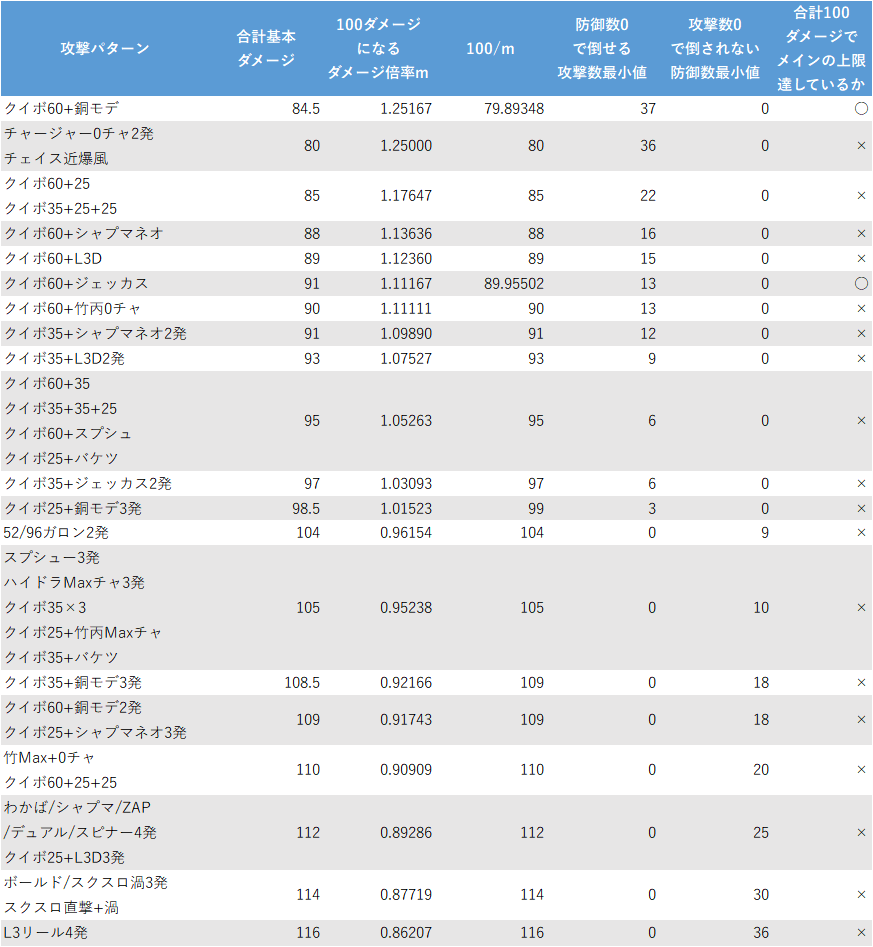
「キューバンボムの爆風+メイン」などここに無い攻撃パターンの確定数推移を知りたい場合には、「100/ダメージ倍率の表」(表2)を使うか、確定数推移の表やグラフを作ってみてください。
初弾のクイボ35
クイボ35については注意が必要です。クイボ35→クイボ60のように、最初にクイボ35があたると、次の図9のように敵のインクを踏みます。よって、安全靴を履いていない場合、スリップダメージが入り合計基本ダメージがずれます。つまり確定数推移がずれるので注意が必要です。安全靴を履いている場合には、クイボ35が当たった後に敵のインクを踏んでもスリップダメージは入らないので問題ないです。また、2発目以降のクイボ35(クイボ60→クイボ35など)でしたら、スリップダメージは入らないので問題ないです。
(安全靴の効果について。安全靴を履いていない場合、蓄積ダメージが50までであればスリップダメージが入ります。安全靴を履いている場合には、蓄積ダメージが30までであればスリップダメージが入ります。)
クイボ25が当たった場合も、たまに敵インクを踏むことがあります。
 図9. クイボ35の塗り跡
図9. クイボ35の塗り跡
9. 確定数推移のグラフ・表(フルバージョン)
では表3に示した攻撃パターンに対する確定数推移のグラフや表を次に示します。
確定数推移のグラフ
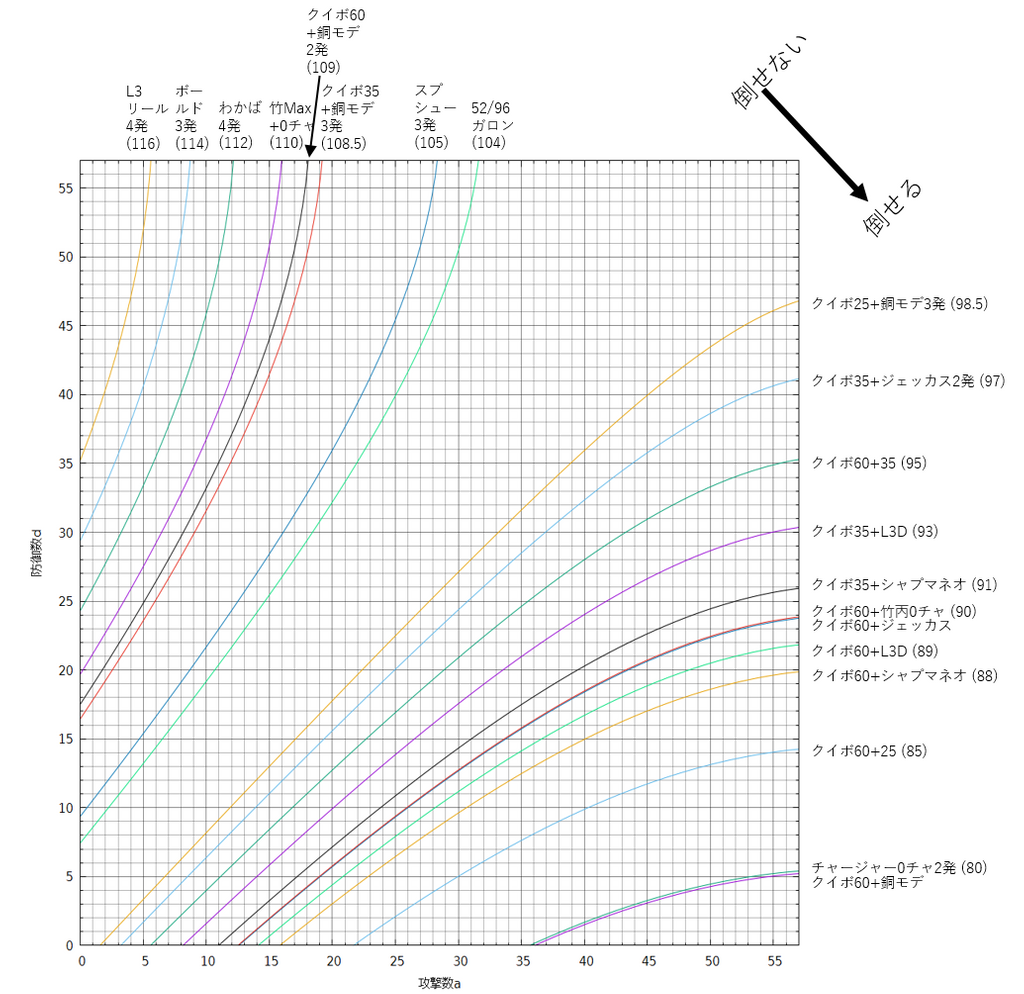 図10. 確定数推移のグラフ (gnuplotのソース)
図10. 確定数推移のグラフ (gnuplotのソース)
括弧内の数字は合計基本ダメージです。図10には各グラフに対して、1種類の攻撃パターンしか書いていないため、書いてない攻撃パターンについては、括弧内の合計基本ダメージを見てグラフを選択してください。例えば、「ハイドラMaxチャ3発」や「クイボ35+バケツ」(どちらも合計基本ダメージは105)の確定数推移のグラフを知りたい場合には、括弧内が105のグラフ(スプシュー3発のグラフ)を選択してください。
ところで、「クイボ60+竹丙0チャ」と「クイボ60+ジェッカス」のグラフがほぼ重なっていますが、完全に重なっているとみなしても問題ありません。なぜならば、次に示す確定数推移の表では「クイボ60+竹丙0チャ」と「クイボ60+ジェッカス」の表の値が完全に一致しているからです。
確定数推移の表
確定数推移の表には次の4つがあります。(xxは表の値)
- 攻撃パターン、攻撃数に対する、倒せる防御数の範囲の最大値(防御数がxx以下だと倒せる)
- 攻撃パターン、攻撃数に対する、倒せない防御数の範囲の最小値(防御数がxx以上だと倒せない)
- 攻撃パターン、防御数に対する、倒せない攻撃数の範囲の最大値(攻撃数がxx以下だと倒せない)
- 攻撃パターン、防御数に対する、倒せる攻撃数の範囲の最小値(攻撃数がxx以上だと倒せる)
この4つの表を順番に提示していきます。攻撃パターンの表記については先程の確定数推移のグラフと同様です。
表4. 攻撃数に対する、倒せる防御数の最大値(防御数がxx以下だと倒せる) 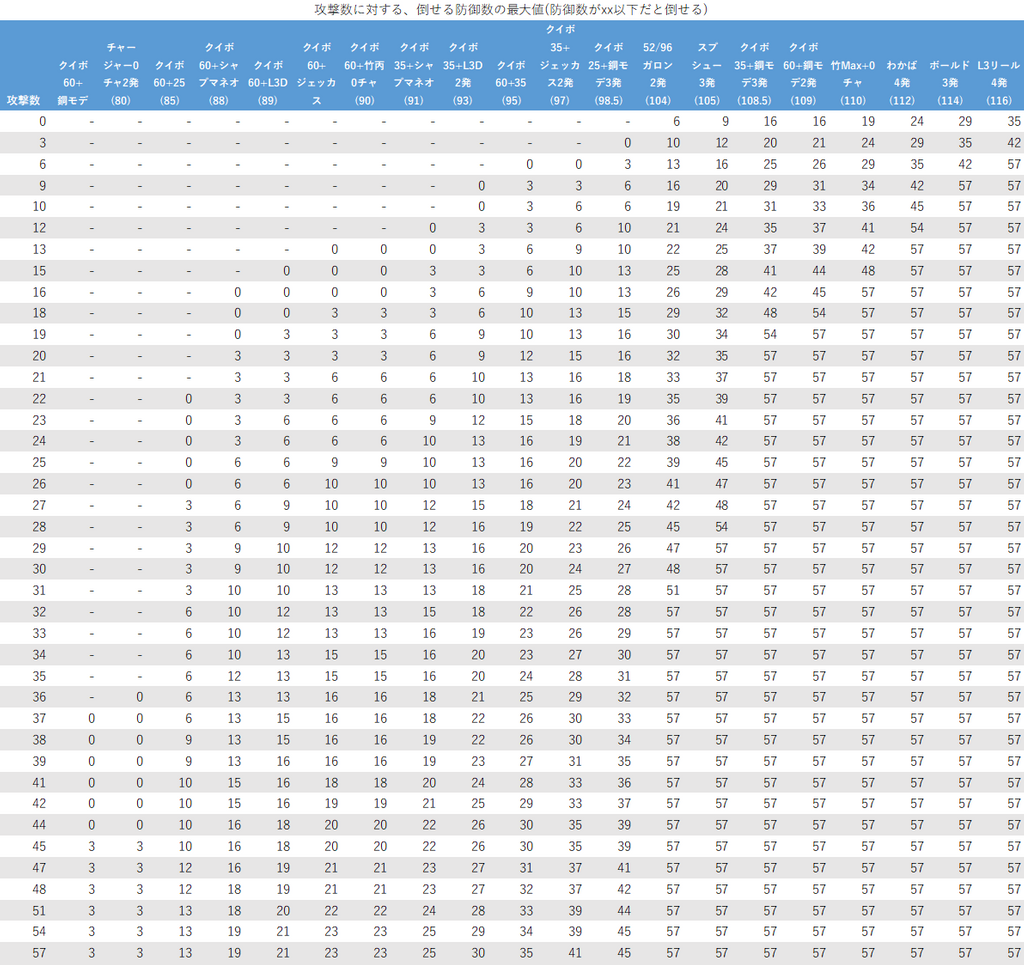
表5. 攻撃数に対する、倒せない防御数の最大値(防御数がxx以上だと倒せない) 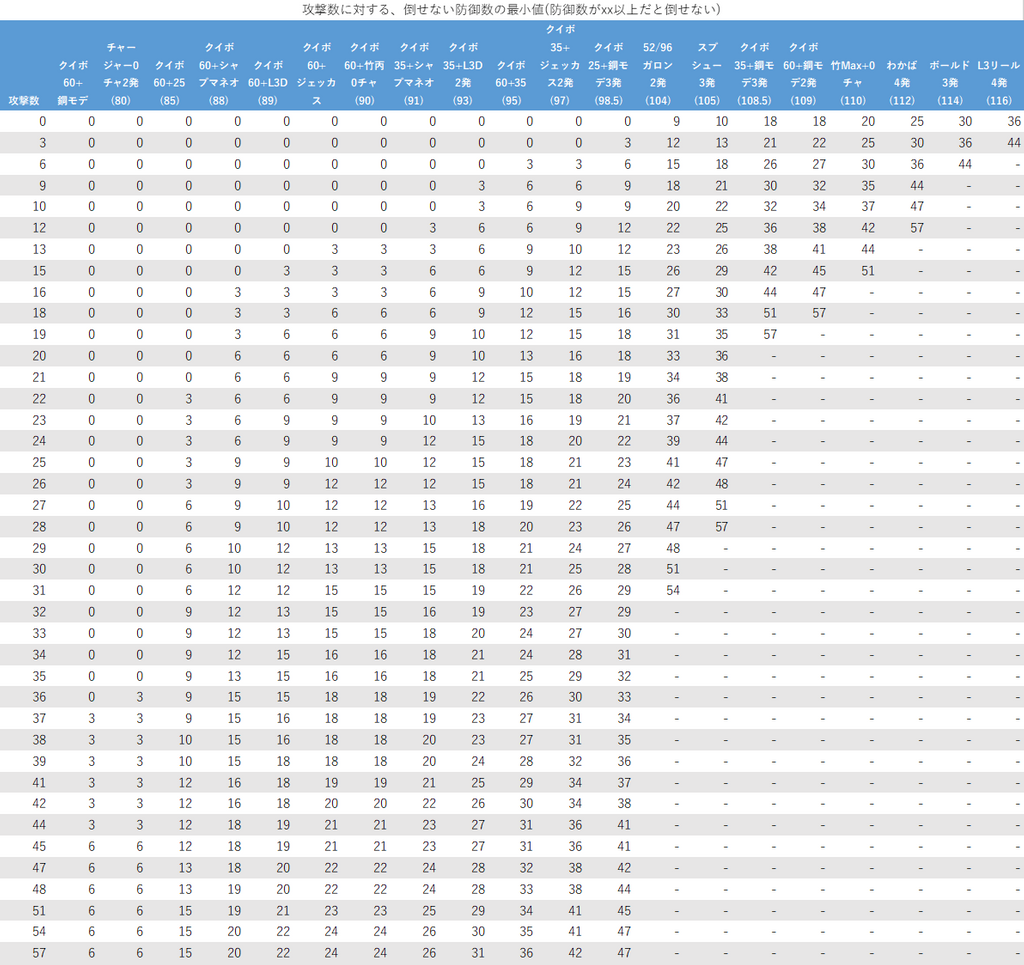
表6. 防御数に対する、倒せない攻撃数の最大値(攻撃数がxx以下だと倒せない) 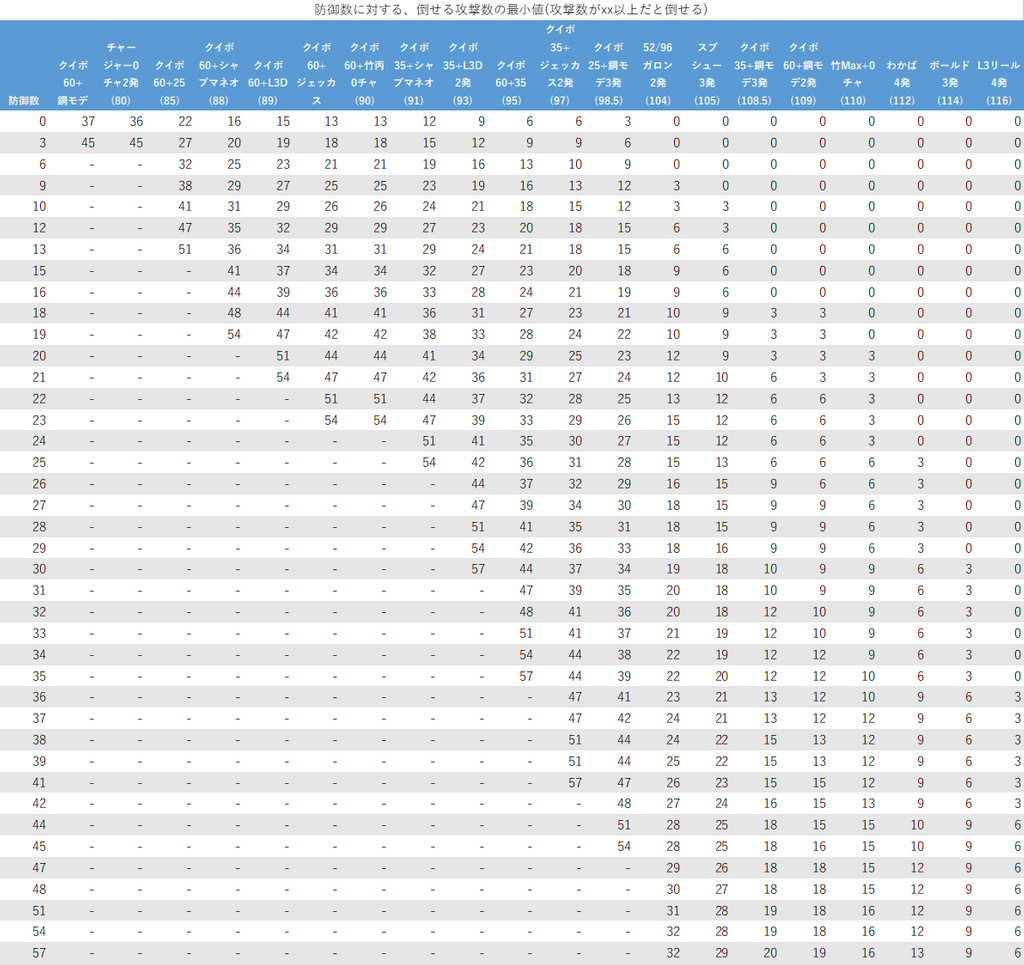
表7. 防御数に対する、倒せる攻撃数の最小値(攻撃数がxx以上だと倒せる)
4つの表のうちどれを使えばいいのかがわかりにくいですが、求めたいのが
- 攻撃数なのか防御数なのか
- xx以下(まで)の範囲なのか、xx以上の範囲なのか
を考えるとよいでしょう。(求めたいのが最大値なのか最小値なのかを考えてしまうと、わけわからなくなります。)
例えば、「防御数がいくつ以上だと倒せなくなるか」を知りたい場合には表5を、「攻撃数がいくつまでだと倒せないか」を知りたい場合には表6を使えば良いとわかります。
表4から表7の4つの確定数推移の表のcsvファイルを置いておきます。→csvファイル
確定数推移の表の不要な攻撃パターンが邪魔で、その攻撃パターンの列を削除したい場合などにはこのcsvファイルを使ってください。
100/ダメージ倍率の表
これについては表2を使えば、どの攻撃パターン(表3に載っていない攻撃パターンも含めて)についても対応できます。
この記事では、倒せる(倒せない)攻撃数(防御数)の範囲(の最大、最小)を求める問題を解く方法として、
- 「確定数推移のグラフ」を使う方法
- 「確定数推移の表」を使う方法
- 「100/ダメージ倍率の表」を使う方法
の3つを紹介してきました。それぞれメリット・デメリットありますので、使いやすい方法を探して使ってみてください。(ちなみに、自分は「確定数推移の表」を使っています。)
10. その他の事柄
知っておくといい(かもしれない)確定数推移に関する事柄について。
ダメージ計算機との違い
「防御32で、敵の攻撃が何積みまでならスプシュー3発を耐えられるか?」のような問題を解くとき、「ダメージ計算ツールを使ってるよ」って人も多いかと思います。確かにダメージ計算機でも求めることができますが、入力を試行錯誤して倒せるかどうかの境界を調べる必要があります。その点、この記事で扱ってきた3つの方法は入力の試行錯誤の必要が無いので、3つの方法のどれかを使うほうが早く求まります。
ダメージ計算ツールは、攻撃数と防御数がすでに決まっていて、その攻撃数と防御数でのダメージや倒せるかどうかを計算するときに使うと良いでしょう。
攻撃と防御のメタの張り合い
まずは合計基本ダメージが100より大きい場合を考えます。確定数推移のグラフ(図10)は合計基本ダメージが100より大きい場合、グラフの傾きが1より大きくなります。このことから、攻撃数を10増やしたときに倒せるようになる防御数の範囲の増加分は、防御数を10だけ増やしたときの倒されなくなる攻撃数の範囲の増加分より大きいです。(例えば、攻撃数を10から20に、防御数を10から20にしたときにどうなるかを考えるとわかります)よって、攻撃と防御のメタの張り合いにおいては防御より攻撃のほうが有利です。また、攻撃数が大きくなるほどグラフの傾きが大きくなるので、攻撃数が大きいほど(防御数が大きいほど)攻撃側がより有利になります。
次に合計基本ダメージが100より小さい場合を考えます。確定数推移のグラフは合計基本ダメージが100より小さい場合、グラフの傾きが1より小さくなります。このことから、攻撃数を10増やしたときに倒せるようになる防御数の範囲の増加分は、防御数を10増やしたときに倒されなくなる攻撃数の範囲の増加分より小さいです。よって、攻撃と防御のメタの張り合いにおいては攻撃より防御のほうが有利です。また、攻撃数が大きくなるほどグラフの傾きが小さくなるので、攻撃数が大きいほど(防御数が大きいほど)防御側がより有利になります。
合計基本ダメージが100より大きいか小さいかで攻撃側が有利になるか、防御側が有利になるかが異なります。
統計データと確定数推移
各プレイヤーのブキと攻撃数と防御数を記録した統計データがあったとします。このとき、次のように割合を用いた主張が可能です。「防御32積みすると、83%のスシコラ、83%の52/96ガロン、62%のダメージ28族の確定数をあげられる」
(ダメージ28族とは、1発が28ダメージである、わかば、シャプマ、ZAP、デュアル、スピナーのことです。)
「防御32積みすると、攻撃16までのスシコラ、攻撃19までの52/96ガロン、攻撃3までの28族の確定数をあげられる」と言うのと、少し違った見方で防御32積みの性能を確認することができます。
サンプル数が385しかなくてあまり使い物になりませんが、各プレイヤーのブキと攻撃数と防御数を記録した統計データを一応置いておきます。→統計データ(csvファイル)
11. いろいろな問題
倒せる(倒せない)攻撃数(防御数)の範囲を求める問題にどのような問題があるかについて整理しておきます。これらの問題は「確定数推移のグラフ」を使っても「確定数推移の表」を使っても「100/ダメージ倍率の表」を使っても解けます。
攻撃数/防御数の性能問題
今まで、「防御32で、敵の攻撃が何積みまでならスプシュー3発を耐えられるか?」という問題のように、すでに決まった自分がつける防御数や攻撃数の性能を知る問題を考えてきました。例えばこの問題で言えば、防御32というのは「攻撃16積みまでであれば敵のスプシュー3発を耐えられる」性能を持っているというのがわかります。この性能を調べておくと、ギアパワーの考察中だけではなく、対戦中にも役に立ちます。例えば、対戦中に攻撃16以下のスプシューがいたら3発耐えられると判断でき、そうでない(攻撃18以上の)スプシューがいたら3発で倒されてしまうと判断できます。
「防御32で、敵の攻撃が何積みまでならスプシュー3発を耐えられるか?」とほぼ同じ問題だが、「防御32で、敵の攻撃が何積み以上だとスプシュー3発を耐えられないか?」という問題も考えられます。
形式的には次の4種類の問題が考えられます。
- 自分の防御数に対して、敵の攻撃数がいくつまでなら倒されないか?
- 自分の防御数に対して、敵の攻撃数がいくつ以上だと倒されるか?
- 自分の攻撃数に対して、敵の防御数がいくつまでなら倒せるか?
- 自分の攻撃数に対して、敵の防御数がいくつ以上だと倒せないか?
攻撃数/防御数決定問題
攻撃数や防御数をいくつつけるかを決定する問題についても同様の考え方で求められます。例えば、「防御32積みが多いから、防御32積みに対してスプシュー3発で倒せるようにしたいが、いくつ以上攻撃を積めばいいか?」という問題が考えられます。この問題は倒せる攻撃数の範囲を求めればよく、これは18以上であると求まります。
形式的には次の2種類の問題が考えられます。
- 敵の防御 積みに対して、倒せるようにするためにはいくつ以上攻撃を積めばよいか?
- 敵の攻撃 積みに対して、倒されないようにするためにはいくつ以上防御を積めばよいか?
2つの攻撃数/防御数の性能比較問題
例えば、「防御数を29にするか32にするか」を決定したいとします。このときには防御29の性能と32の性能を比較できると決定しやすくなります。では「防御29と32の性能の違いはなにか?」という性能比較問題について考えます。この問題については(マイナーなものを除いた)各攻撃パターンに対してそれぞれ、攻撃数がいくつまでであれば耐えられるかを調べればよいでしょう。例えば、スプシュー3発の場合、防御29だと攻撃15耐えられます。また、防御32だと攻撃16まで耐えられます。
同じようなことですが、「防御29で倒されて防御32で倒されないような各攻撃パターンに対する攻撃数」を調べても良いでしょう。スプシュー3発の場合、そのような攻撃数は16です。
12. 練習問題
これらの問題は慣れないと解くのが大変なので、最後に練習問題を載せておきます。「確定数推移のグラフ」を使っても「確定数推移の表」を使っても「100/ダメージ倍率の表」を使っても大丈夫です。好きな方法で解いてください。
Q1. 防御25積みで、敵の攻撃数がいくつまでであれば「クイボ60+35」を耐えられるか?
**Q2.**攻撃サブ1のダメージ28族(わかば、スピナーなど)の確定数を上げるためには防御をいくつ積めばよいか?
Q3. 防御サブ1で倒されなくて、防御なしで倒される場合はどのような場合か?(そのような敵の攻撃パターンと攻撃数は?)
A1. 35まで
A2. 攻撃サブ1は57表記で3である。なので、攻撃3の「わかば4発」を耐えれる防御数はいくつ以上かを求めれば良い。これは防御30以上なので、防御を30以上積めば良い。
A3. 攻撃22から26積みの「クイボ60+25」、攻撃6積みの「クイボ60+35」など。(52/96ガロンやスプシュー、ダメージ28族などの攻撃パターンでは防御3積みしたところで確定数が上がるわけではないので、防御0と防御3との差は出ない。合計基本ダメージが100未満だと、防御0と防御3の差が出やすい。)
13. 参考にしたサイト
ギアパワー検証 - スプラトゥーン(Splatoon) for 2ch Wiki*
ダメージ倍率計算式や確定数推移のグラフやその作り方などはこのWikiのページを参考にしました。