この記事は新歓ブログリレー2020 37日目の記事です。

こんにちは。algorithm班のidatenです。普段は、競技プログラミングをしています。今回は、競技プログラミングで使う際に、Rolling Hashというアルゴリズムの衝突の話と、基数にランダムな原始根を使ってみるという話をしようと思います。

Rolling Hashとは

文字列(もしくは数列)をHash値に変換することで、文字列同士の比較を$O(1)$ですることができるようになります。これによって、文字列の検索や比較が高速に行うことができます。

詳しくは、蟻本p.332かラビンカープ法のおはなし+二次元のロリハいいぞの1,2,3章を参照してください。

Hashの衝突

以下ではRolling Hashで使う素数を$p$、基数を$b$とします。

Hash値を用いて文字列を比較する場合、「Hash値が等しいならば、下の文字列も等しい」という前提を置いていますが、実際は成り立ちません。異なる文字列であるが、同じHash値となってしまうことをHashの衝突といいます。
しかし、実際には高い確率で判定できることと高速に動作することから、プログラミングコンテストにおいてよく使われています。

素数$p$を用いた際のHashの衝突確率についてもう少し詳しく見てみます。
まず、二つ文字列を比較する場合と文字列の種類数を求める場合に大別できて、

• 二つの文字列の比較の場合

比較を1回行う際に衝突する確率は大体$1/p$なので、$n$回比較するとすると、$\text{prob}=1-(1-1/p{)}^n$となり、$p=10^9,n=10^5$程度のとき

$\text{prob}\simeq 0.00010=0.010\%$となり、これは実用上ほぼ問題ない値です。

ただし、これはケースが作為的に選ばれた場合は成り立ちません。後述のように$p$や$b$を固定すると、わざと衝突させることができるようです。

• 文字列の種類数を求める場合

これはいわゆる誕生日のパラドックスというもので、1つでも衝突したら種類数が正しく求まらなくなるので感覚よりもずっと高い確率で衝突します。$n$個の異なる文字列のHash値を求めるとして、それぞれの1つ同士の衝突確立が大体$1/p$です。このとき、$n$個のHash値全てが異なる確率$\text{unique}(n,p)$は、(0-indexで)$0$個目から考えると$i$個目が$j(<i)$個目と異なるHash値である確率は$(p-i)/p$であるから

$$\text{unique}(n,p)=\prod _{i\in [0,n)}\frac{(p-i)}{p}=\frac{p!}{(p-n)!p^n}$$

となります。$p=10^9,n=10^5$程度のとき、$\mathrm{u}\mathrm{n}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{e}(n,p)\simeq 0.0067$であり^[1]、衝突確率$\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}(n,p)=1-\text{unique}(n,p)\simeq 0.9933=99.33\%$とほぼほぼ衝突するということがわかります。

詳しく知りたい方は、

• ハッシュの衝突 - あなたは嘘つきですかと聞かれたら「YES」と答えるブログ
• 誕生日攻撃 - Wikipedia

を参照してください。

こうしてみると、二つの文字列の比較の場合は安全そうですが、種類数の場合は結構危うそうです。

そのため、$p$や$b$の取り方を工夫して、衝突確率を下げる工夫がなされていることもあります。
例えば、

• $p$もしくは$b$を複数用意してhash値が全ての場合で、一致しているかみる
• $p$を大きくして$1/p$を小さくする

などがあります。

また、今回の主題に関わってくることですが、比較を1回行う際に衝突する確率は大体$1/p$としましたが、これは後述の通り、$b$の値によって変わり、その際に$b$が$p$の原始根であった場合、衝突確率$p$は$1/p$となりますが、そうでない場合、衝突確率は上がります。

原始根とは

原始根を次のように定義します。

原始根の定義と具体例 | 高校数学の美しい物語

（$3$以上の）素数$p$と$1$以上$p$未満の整数$r$が以下の性質を満たす時$r$を法$p$に対する原始根と呼ぶ。
「$r,r^2,\dots ,r^{p-2}$のいずれもが$p$で割ってあまり$1$でない」
（また、$r=1$は$p=2$に対する原始根である, とする）

例えば、法が$13$の場合$r^i(\mathrm{m}\mathrm{o}\mathrm{d}13)$の値の表は以下の通りです。この表より、$2,6,7,11$が原始根であることがわかります。

また、周期がそれぞれ$p-1=12$の約数である$1,2,3,4,6,12$のいずれかであることが見て取れます。

このように、$b$が$p$の原始根でない場合、$b^i(\mathrm{m}\mathrm{o}\mathrm{d}p)$が同じ値である$i$が存在し、原始根の場合は、$b^i(\mathrm{m}\mathrm{o}\mathrm{d}p)$は$i\in [0,p-1)$において一意的(重複が存在しない)です。そこで、$b$を$p$の原始根にすることで、衝突の確率を下げよういうのが狙いです。

素数$p$の決め方

今回の主題ではないですが、$b$の決め方と両立できるので軽く書きました。

なるべく大きくしたいという点と計算のしやすさから$p$は$10^9$付近の素数、もしくは安全で爆速なRollingHashの話 - Qiitaのように$2^{61}-1$を使うことが多いです。

この$p=2^{61}-1$を使う話は、かなり強力なので是非読んでみてください。

基数$b$の決め方

今回は$b$の決め方について、書いてみようと思います。多くの場合、$b$は乱数で生成します。固定値だとコンテスタントがhackできるタイプのコンテストで衝突するケースを生成することができるそうです。
参考：Rolling Hashを殺す話 | SlideShare

しかし、単純な乱数生成では、運が悪いとすぐ衝突するような良くない乱数が生成されてしまうかもしれません。

そこで、$b$の値として原始根をランダムに生成することで、安全かつhackされにくくします。

奇素数$p$の原始根$r$

ここからが主題です。長くなってすみません。

整数を$m\in \mathbb{Z}$で割った余りの集合を剰余類と呼び$\mathbb{Z}/m\mathbb{Z}$と表します。剰余類の内、$m$と互いに素なものの集合を$(\mathbb{Z}/m\mathbb{Z}{)}^{\times }$と表します。

原始根の性質

ここで、素数$p$の原始根$r$が一つ分かっているとします。

このとき、次が成り立ちます。

1. $(\mathbb{Z}/p\mathbb{Z}{)}^{\times }=\{r^0,r^1,\dots ,r^{p-2}\}$
2. $r^k$が$p$の原始根 $\iff$ $p-1$と$k$が互いに素

1の証明は原始根の定義と具体例（高校生向け） - 高校数学の美しい物語
の原始根の重要な定理を参照してください。

2の証明は流れを書くと、1の$r$を$r^k$に置き換えるとそれぞれ$(r^k{)}^i=r^{ki}$になることと、Fermatの小定理から$r^{p-1}\equiv 1$であるので、指数の肩は$(\mathbb{Z}/(p-1)\mathbb{Z})$上の演算と考えることができることから導けます。

上の議論より、素数$p$の原始根が1つわかっていれば、$p-1$と互いに素な自然数$k$をランダムに生成してRolling Hashの基数$b$を$r^k$とすればいいことがわかります。それでは、自然数$k$を見つけるのにどれくらい時間がかかるのでしょうか。

ここでは、自然数$k$を$p-1$以下とします。$1$以上$p-1$以下で$p-1$と互いに素な自然数の個数は、オイラーの$\phi$関数を用いて、$\phi (p-1)$個であるので、$k$が$p-1$と互いに素な確率は、$\phi (p-1)/(p-1)$です。

代表的な素数の値を載せておきます。

• $p=10^9+7$,
  $\phi (p-1)/(p-1)=0.5$
• $p=2^{61}-1$,
  $\phi (p-1)/(p-1)=0.176277$

実際に自分が使う素数の値を求めてみるといいと思いますが、上記の素数を使う場合$p-1$と互いに素な自然数を乱数で見つける期待値は、実用的に定数回と言っていいレベルです。

以上より原始根があらかじめ一つ分かっていれば($r$とします)、ランダムに原始根を実行時に生成することができます。

次の手順です。

1. 自然数の乱数$k<p-1$を発生させる。
2. $k$と$p-1$が互いに素であるか確認する。互いに素でないなら1.に戻る。
3. $r^k(\mathrm{m}\mathrm{o}\mathrm{d}p)>A$であることを確認する。そうでないなら1.に戻る。
4. $b=r^k(\mathrm{m}\mathrm{o}\mathrm{d}p)$に設定する。

追記：ただし、数列の最大値を$A$として、$b\le A$の時、次の2つの数列が衝突してしまいます。
$\{1,0\},\{b\}$
そのため、$b>A$である必要があります。そこで上記手順に3を足しました。
ただ、一般に$A\ll p$であるため、「$k$が$p-1$と互いに素」かつ「$r^k(\mathrm{m}\mathrm{o}\mathrm{d}p)>A$」である確率はほぼ上記と同じでしょう。

原始根を一つ求める

原始根を一つ求めてみます。基数を実行時に決定するため、素数$p$を実行時に決定するのはあまりうまみがないので、素数$p$を定数とします。

すると、コンテストの前にプログラムを動かして自分のRolling Hashでつかう素数に対して一つ求まっていればいいです。

例として、$p=2^{61}-1\simeq 10^{18}$の原始根を求めてみます。

原始根の求め方ですが、一つの方法として$1$から順に、$1$乗から$p-2$乗して$1$になるかどうかを確かめるという方法がありますが、判定で$O(p)$かかるので現実的ではありません。

そこで、次の事実を利用します。$m\in (\mathbb{Z}/(p-1)\mathbb{Z})$において$m^j\equiv 1(j\ne p-1)$となるような$j$が存在するとき、$j$は$p-1$の約数に限る。

これは、Fermatの小定理から導けます。

これを利用して、
$p-1$を素因数分解すると
$p-1=2^1\cdot 3^2\cdot 5^2\cdot 7^1\cdot 11^1\cdot 13^1\cdot 31^1\cdot 41^1\cdot 61^1\cdot 151^1\cdot 331^1\cdot 1321^1$
となるので、$n$の約数の個数を$d(n)$として、$d(p-1)=9216$個調べればいいことがわかります。

また、原始根の性質2. より、原始根の数は$|(\mathbb{Z}/(p-1)\mathbb{Z}{)}^{\times }|=\phi (n)$と等しいので、原始根が見つかるまでの期待計算量は、判定に$O(d(p-1))$かかるので$O(d(p-1)p/\phi (p-1))$となります。

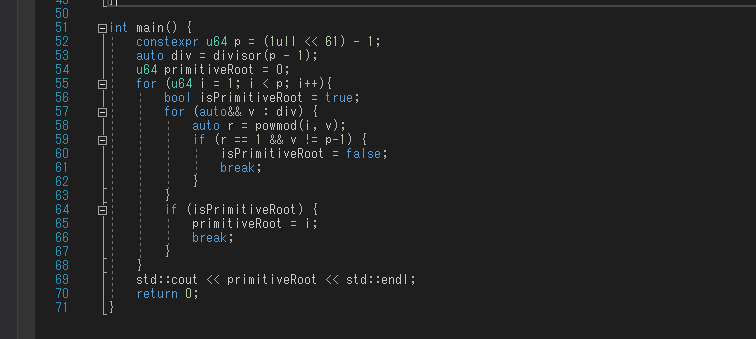
原始根を求めるコードをC++で実装しました。以下がそのソースコードです。原始根はたいていすぐ見つかるので素因数分解がボトルネックで$O(\sqrt{N})$だと思います。($p>3\ast 10^9$なのでオーバーフローを回避するためにmul関数が特殊です。$p\le 3\ast 10^9$ならコメントアウトしたほうのmulが使えます)
※(2021/9/1　コメントで指摘があった通り，コードが間違っていたため修正しました．)

#include <iostream>
#include <vector>

using u64 = uint64_t;

template<typename T>
std::vector<T> divisor(T n) {
	std::vector<T> res1;
	std::vector<T> res2;

	for (T i = 1; i * i <= n; i++) {
		if (n % i == 0) {
			res1.push_back(i);
			if (i != n / i) {
				res2.push_back(n / i);
			}

		}
	}
	for (u64 i = res2.size(); i  >0; --i){
		res1.push_back(res2[i - 1]);
	}
	return res1;
}
//*
u64 mul(u64 a, u64 b) { // a*b mod 2^61-1
	constexpr u64 p = (1ull << 61) - 1;
	const u64 m30 = (1ull << 30) - 1;
	const u64 m31 = (1ull << 31) - 1;
	u64 au = a >> 31;
	u64 ad = a & m31;
	u64 bu = b >> 31;
	u64 bd = b & m31;
	u64 mid = ad * bu + au * bd;
	u64 midu = mid >> 30;
	u64 midd = mid & m30;
	u64 res = ((au * bu * 2) % p + midu + (midd << 31) % p + (ad * bd) % p) % p;
	return res;
}
/*/
//*
constexpr u64 p = 998244353;

u64 mul(u64 a, u64 b) {
	return ((a % p) * (b % p)) % p;
}
//*/
u64 powmod(u64 base, u64 exp) { // base^exp mod MOD
	if (exp == 0) {
		return 1;
	} else if (exp % 2 == 0) {
		u64 t = powmod(base, exp / 2);
		return mul(t, t);
	} else {
		return mul(base, powmod(base, exp - 1));
	}
}

int main() {
	constexpr u64 p = (1ull << 61) - 1;
	auto div = divisor(p - 1);
 	u64 primitiveRoot = 0;
	for (u64 i = 1; i < p; i++){
		bool isPrimitiveRoot = true;
		for (auto&& v : div) {
			auto r = powmod(i, v);
			if (r == 1 && v != p-1) {
				isPrimitiveRoot = false;
				break;
			}
		}
		if (isPrimitiveRoot) {
			primitiveRoot = i;
			break;
		}
	}
	std::cout << primitiveRoot << std::endl;
	return 0;
}

実行結果より、$p=2^{61}-1$の原始根の一つは$37$であることがわかります。

まとめ

記事の内容をまとめると次の通りです。

• 素数$p$は計算の都合が許す限り大きい方がいい
• 基数$b$は固定しない方がよく、原始根の方が安心
  • 原始根でも数列の要素の最大値より小さいと自明な衝突があるので駄目
• 原始根のランダムな取り方は次の手順
  1. 素数$p$を決める
  2. 素数$p$に対し、原始根$r$を一つ求める(ここまでは事前準備）
  3. 実行時に、$p-1$と互いに素かつ$r^k(\mathrm{m}\mathrm{o}\mathrm{d}p)>\max (a)$な整数$k$を一つ求める。（文字列(数列)を$\{a\}$とします。）
  4. 基数$b$を$b=r^k(\mathrm{m}\mathrm{o}\mathrm{d}p)$として定める

参考文献

1. maspyさん [AtCoder 参加感想] 2019/09/14:ABC 141
2. tsujimotterさん 原始根の数のかぞえかた

すでにこのページでリンクを貼っているサイトは省略させていただきました。

おわりに

今回はRolling Hashのアルゴリズムで基数をランダムな原始根にする方法を解説しました。間違いなどありましたら、気軽にご指摘ください。

明日の担当者は@kano @Kejunです。おたのしみに。

[1]
$\mathrm{u}\mathrm{n}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{e}(10^5,10^9)$を求める問題は、つい最近のABC156 D - Bouquetでほぼ同じ問題がでましたね。