こんにちは。SysAd班・CTF班に所属している 20Bのtessoです。
この記事は5/1に開催されたCPCTF22の作問者writeupです。

私は PHE1, PHE2, Robotsの3問を作問しました。ご参加ありがとうございます。

writeup

• Web/Robots (Newbie)
• Crypto/PHE1 (easy)
• Crypto/PHE2 (medium)

Robots

Newbie
10.00pt / 59 solved
正答者数

問題

Robots.txtをのぞいてみましょう。
https://chocolatechipcookie.cpctf.space/

解法

https://chocolatechipcookie.cpctf.space/robots.txtにアクセスしてみます。すると以下の文章がブラウザに表示されます。

# こんにちは、ここがrobots.txtです
User-agent:*
Disallow: /flag_h7Mz.html

Disallowにある /flag_h7Mz.html にアクセスすると flagを得ることができます。

robots.txtに関するより詳細な内容は、次のリンクを見てください。

robots.txt の概要とガイド | Google 検索セントラル | ドキュメント | Google Developers

robots.txt は、クローラのトラフィックを管理するために使用されます。この robots.txt の概要ガイドでは、robots.txt ファイルの基本とその使用方法について説明します。

Google Developers

PHE1

Easy
184.28pt / 43 solved
正答者数

問題

秘密鍵を持ってることを秘密鍵なしで証明するハッピーな方法を考えたッピ！

# coding: utf-8
import os
from Crypto.Util.number import getPrime, bytes_to_long

from secret import flag


def encrypt(plain, N, e):
    return pow(plain, e, N)


def decrypt(enc, p, q, e):
    phi = (p-1) * (q-1)
    d = pow(e, -1, phi)
    return pow(enc, d, p * q)


def generate_question(N, e):
    question1 = bytes_to_long(os.urandom(16))
    question2 = bytes_to_long(os.urandom(16))
    question3 = question1 * question2

    return [encrypt(question1, N, e), encrypt(question2, N, e)], encrypt(question3, N, e)


def main():
    p = getPrime(512)
    q = getPrime(512)
    N = p * q
    e = 0x10001

    print("Welcome to Happy App")
    print(f"N = {N}")
    print(f"e = {e}")
    while True:
        q, correct = generate_question(N, e)
        print(f"encrypt(a) = {q[0]}")
        print(f"encrypt(b) = {q[1]}")
        print("What is a × b encrypted")

        answer = int(input("> "))
        if(correct == answer):
            print(flag)
        else:
            print("Noooooo")
        break
    return


if __name__ == "__main__":
    main()

解法

この問題はRSA暗号の乗法準同型性を利用しています。

RSA 暗号では、同じ公開鍵で暗号化されたもの同士を掛け算することで、平文同士を掛け算したものの暗号文を得ることができます。

以下のように式変形をすることで確かめることができます。

$$
N,e:公開鍵\\
a,b:平文
$$

$$
\begin{aligned}
encrypt(a) &= a ^ e \bmod N\\
encrypt(b) &= b ^ e \bmod N\\
encrypt(a) * encrypt(b) &= (a \times b) ^ e \bmod N \\
&= encrypt(a \times b)
\end{aligned}
$$

今回は、 a * b  を暗号化したものは何かを問われているので、乗法準同型性を利用して encrypt(a * b) を求め、送信することでFlagが得られます。

お気持ち

暗号文を復号することなしに、任意の演算を行うことを許す暗号を準同型暗号(Homomorphic Encryption)といいます。また、任意でなく部分的に演算できるものをPartially homomorphic encryptionといいます。問題名は、その頭文字をとっています。RSAでは、乗法のみ可能なのでPHEです。

準同型暗号の歴史はかなり面白いので、興味があったらwikipediaを読んでみてください。

Homomorphic encryption - Wikipedia

Wikimedia Foundation, Inc.Contributors to Wikimedia projects

RSAの乗法準同型性に関して、RSA暗号そのものの安全性を考えてみましょう。乗法準同型性を持つので、RSA暗号には頑強性がありません。一般に、暗号には持つべき性質として 一方向性、 強秘匿性、頑強性があります。一方向性とは、暗号文が与えられたときに、平文を推測できないことを言います。強秘匿性は暗号文から元の平文の情報を得られないことを言います。そして、頑強性とは、暗号文から別の暗号文を作れないことを言います。明らかにRSA暗号は、頑強性がありません。もちろん、すでに頑強性に対する改良がされており、現在では改良したRSA暗号が利用されています。ここら辺の話は、次のリンクに詳しい話があります。

クラウドを支えるこれからの暗号技術

PHE2

Medium
388.15 / 8 solved
正答者

問題

新しい電子投票システムを使って、信任投票を行うみたいです。
この信任投票では、１票でも賛成であれば、承認されます。
どうやら、この信任投票を阻止すると特別なメッセージを受け取れるらしいです。

# coding: utf-8
from Crypto.Util.number import getPrime, inverse, getRandomRange
import math
from secret import flag


def lcm(a, b):
    return (a * b) // math.gcd(a, b)


class Cryptosystem:
    def __init__(self, bits):
        p = getPrime(bits // 2)
        while True:
            q = getPrime(bits // 2)
            if p != q:
                break
        n = p * q
        λ = lcm(p - 1, q - 1)
        while True:
            g = getRandomRange(2, n * n)
            μ = inverse((pow(g, λ, n * n) - 1) // n % n, n)
            if μ is not None:
                break
        self.secret_key = (λ, μ)
        self.public_key = (n, g)

    def encrypt(self, plain):
        n, g = self.public_key
        nn = n * n
        assert(0 <= plain < n)
        while(True):
            r = getRandomRange(2, n)
            if(math.gcd(r, n) == 1):
                break
        return (pow(g, plain, nn) * pow(r, n, nn)) % nn

    def decrypt(self, crypto):
        n, _ = self.public_key
        λ, μ = self.secret_key
        return ((pow(crypto, λ, n * n) - 1) // n * μ) % n


class OnlinePoll:
    def __init__(self):
        self.cryptosystem = Cryptosystem(bits=1024)
        self.votes = self.cryptosystem.encrypt(100)

    def vote(self, crypto):
        n, _ = self.cryptosystem.public_key
        nn = n * n

        if(crypto * self.votes % nn == 0):
            return -1

        self.votes = crypto * self.votes % nn

    def result(self):
        ret = self.cryptosystem.decrypt(self.votes)
        return ret


def main():
    onlinepoll = OnlinePoll()
    n, g = onlinepoll.cryptosystem.public_key
    one = onlinepoll.cryptosystem.encrypt(1)
    zero = onlinepoll.cryptosystem.encrypt(0)

    print("Welcome to OnlinePoll System")
    print("public keys...")
    print(f"n = {n}")
    print(f"g = {g}")
    print("")
    while True:
        print("Enter one if you agree and zero otherwise.")
        print(f"one = {one}")
        print(f"zero = {zero}")
        vote = int(input(">"))
        err = onlinepoll.vote(vote)

        if(err == -1):
            print("illegal input.")
            continue

        print("Election Results...")
        result = onlinepoll.result()
        print(f"Approve: {result}")
        if(result != 0):
            print("He won this vote.")
            print("Thank you for voting.")
        else:
            print("He lose this vote.")
            print("Thanks for your cooperation.")
            print(f"{flag}")
        break


if __name__ == "__main__":
    main()

解法

この問題では Paillier暗号 (ぺいえあんごう) の加法準同型性を利用しています。Paillier暗号では、暗号文同士を掛け算することで、暗号文同士を足し算したものを暗号化したものを得られます。

今回の問題では、1票でもあれば承認されてしまいます。つまり、賛成票を０にすればよいわけです。プログラムの OnlinePoll.vote にて、うまく操作して、OnlinePoll.votesを、0を暗号化したものにできないかと考えます。Paillier暗号の加法準同型性を利用して、足して０になるように考えます。平文を0にするためには、合同式であることを利用して、$N^2$にするとよさそうです。

幸いに入力では、oneとzero以外にも受け取ってくれそうなので、$N^2−100$を暗号化したものを入力します。OnlinePoll.votes には、$N^2$を暗号化したものが保存されます。復号した際には、0と合同なので０として認識されます。
賛成票を0にすることができたのでFlagを得ることができました。

お気持ち

PHE1のお気持ちで表明した通り、この問題も準同型性を暗号に関する問題です。今回は、加法が成立します。Flagは CPCTF{7h3_11f73d-3194m41_c2yp705y573m_15_4150_4n_4dd171v3_h0m0m02ph1c_c2yp705y573m} です。原文は、 The Lifted-ElGamal cryptosystem is also an additive homomorphic cryptosystem. です。Paillier暗号以外にも ElGamal暗号を少しいじったLifted-ElGamal暗号でも加法準同型性が成り立ちます。

準同型暗号の最前線2（原理編） - Qiita

初めに この記事は準同型暗号の最前線1（入門編）の続きです。私たちが提案したL2準同型暗号の原理を解説します。 金庫開けクイズ まず簡単なクイズから始めましょう。ここに金庫があり、その金庫には24個の歯があるダイヤルが...

Qiitaherumi

問題の題材になっている電子投票を考えてみます。今回のシステムは、以下の様に考えるとより実用的になります。

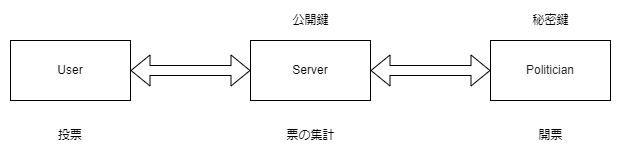
選挙を考えれば以下の対応が考えられます

User：国民
Server：選挙管理委員会
Politician：政治家

まず、Politicianは秘密鍵と公開鍵を生成します。公開鍵はServerに渡します。
Serverは、oneとzeroを生成し、Userに送信します。
Userは、Serverから渡された表のうち好きな方を送信します。
Serverは、送信結果と手元の票を足します。
選挙が終わり次第、ServerはPoliticianに集計した票を送信します。

このモデルでは、ServerとPoliticianは健全な関係を築いていると仮定するとうまく動作します。

Politicianは何票得たのかのみ知ることができ、どのUserから何を受け取ったかを知る余地はありません。

今回のシステムのダメなところは、入力にoneとzero以外を受け取ってしまうところです。なので、投票されたのはoneなのかzeroなのかをいい感じに調べなくてはなりません。シンプルな実装としては、提供したoneとzeroを比較すればよいですが、投票結果が第３者に漏れてしまうので論外です。そこで、ゼロ知識証明が必要になります。ゼロ知識証明として以下の動画や、記事が面白いですね。

暗号解説シリーズ　「ゼロ知識証明」について解説！！ - Qiita

ゼロ知識証明 古い技術：ゼロ知識対話証明（とてもわかりやすいのでぜひご覧ください。）でも紹介されているように、「ゼロ知識証明」は1980年代に発表された技術です。ユーザー認証を安全に行うという目的のもと開発された技術で、RSA...

Qiitakenmaro

さいごに

全体的に知っていれば解けるけど、知らないと解けないみたいなひねりがないクソ問題になってしまいました。ごめんなさい。来年はひねりがある問題を作ります。

お気持ちの部分はまとめ記事になってしまいました。少しでも面白そうだなって思ったらリンクを踏んでみてください。

CPCTF22へのご参加ありがとうございます。他にもCPCTF関連の記事が投稿されると思うので、見てみてください！